ফিকের ব্যাপন সূত্র

আণবিক বিসরণ কে মাইক্রোস্কোপিক এবং ম্যাক্রোস্কোপিক দৃষ্টিকোণ থেকে দেখা হয়েছে। প্রথমে, একটি প্রতিবন্ধক (বেগুনি রেখা) দ্বারা বিভক্ত পাত্রের বাম পাশে শুধুমাত্র দ্রাবক অণুগুলি রয়েছে এবং ডান পাশে কিছুই নেই। প্রতিবন্ধকটি সরিয়ে দেওয়ার পর, দ্রাবকটি পুরো পাত্রে বিস্তৃত হয়ে যায়। শীর্ষ: একক একটি অণু এলোমেলোভাবে চলাচল করে। মধ্যম: আরও বেশি অণু থাকলে, দ্রাবকটি পাত্রে আরও সমভাবে ছড়িয়ে পড়ে এবং একটি পরিষ্কার প্রবণতা তৈরি হয়। নিচের চিত্র: বিপুল সংখ্যক দ্রাবক অণুর সঙ্গে এলোমেলো গতি দৃশ্যমান হয় না; দ্রাবকটি উচ্চ ঘনত্বের স্থান থেকে কম ঘনত্বের স্থানে মসৃণ ও সুনির্দিষ্টভাবে প্রবাহিত হয়। এই মসৃণ প্রবাহটি ফিকের সূত্র দ্বারা বর্ণিত হয়।

ফিকের ব্যাপন সূত্র ব্যাপন সম্পর্কে বর্ণনা করে। প্রধানত পরীক্ষামূলক ফলাফলের উপর ভিত্তি করে ১৮৫৫ সালে প্রথমবারের মতো এটি আদলফ ফিক দ্বারা প্রস্তাবিত হয়েছিল। এই সূত্রগুলি ভর-ব্যাপন সহগ টেমপ্লেট:Mvar নির্ধারণে সাহায্য করতে পারে। ফিকের প্রথম সূত্রটি তার দ্বিতীয় সূত্রের প্রাপ্তির জন্য ব্যবহৃত হয়, যা ব্যাপন সমীকরণ এর সমান।

ফিকের প্রথম সূত্র: কণার উচ্চ ঘনত্ব থেকে নিম্ন ঘনত্বে চলাচল (বায়ুপথের মাধ্যমে বিস্তার) কণার ঘনত্বের গ্রেডিয়েন্টের সাথে সরাসরি আনুপাতিক।

ফিকের দ্বিতীয় সূত্র: বিস্তারজনিত কারণে সময়ের সাথে ঘনত্বের গ্রেডিয়েন্টে পরিবর্তনের পূর্বাভাস।

যে ব্যাপন প্রক্রিয়া ফিকের সূত্র মেনে চলে, তাকে স্বাভাবিক বা ফিকিয়ান ব্যাপন বলা হয়; অন্যথায়, তাকে অস্বাভাবিক বা নন-ফিকিয়ান ব্যাপন বলা হয়।

ইতিহাস

১৮৫৫ সালে শারীরবিদ অ্যাডলফ ফিক তার সূত্রগুলি প্রথম বর্ণনা করেন, যা ডিফিউসিভ প্রক্রিয়ায় ভরের পরিবহন সম্পর্কিত তার সূত্রগুলো ব্যাখ্যা করে। ফিকের এই কাজটি পূর্বে থমাস গ্রাহাম-এর পরীক্ষাগুলির দ্বারা প্রভাবিত ছিল, যদিও সেগুলি ফিকের পরিচিত সূত্রগুলির ভিত্তি তৈরি করতে সক্ষম হয়নি। ফিকের সূত্রটি একই সময়ে অন্য বিশেষজ্ঞ বিজ্ঞানীদের আবিষ্কৃত সূত্রগুলির মতো, যেমন: ডার্সির সূত্র (হাইড্রোলিক প্রবাহ), ওহমের সূত্র (চার্জ পরিবহন), এবং ফুরিয়েরের সূত্র (তাপ পরিবহন)।

ফিকের পরীক্ষা (যা গ্রাহামের পরীক্ষার আদলে করা হয়েছিল) লবণের ঘনত্ব এবং প্রবাহ পরিমাপের সঙ্গে সম্পর্কিত ছিল, যা দুটি জলাধারের মধ্যে পানি দিয়ে তৈরি নলিকাগুলির মাধ্যমে ডিফিউজ হচ্ছিল। এটি লক্ষ্যণীয় যে, ফিকের কাজ মূলত তরলগুলিতে ডিফিউশন সম্পর্কিত ছিল, কারণ সে সময়ে কঠিন পদার্থে ডিফিউশন সাধারণত সম্ভব বলে বিবেচিত হতো না। আজকাল, ফিকের সূত্রগুলি কঠিন, তরল এবং গ্যাসে ডিফিউশনের আমাদের বোঝাপড়ার মূল স্তম্ভ হিসেবে প্রতিষ্ঠিত হয়েছে (যখন শেষ দুটি ক্ষেত্রে বাল্ক তরল গতির অভাব থাকে)। যখন কোনো ডিফিউশন প্রক্রিয়া ফিকের সূত্র অনুসরণ করে না (যা পোরাস মিডিয়া দিয়ে ডিফিউশন এবং স্ফীতির প্রবাহকারী পদার্থের ডিফিউশনসহ অন্যান্য ক্ষেত্রে ঘটে), সেটিকে নন-ফিকিয়ান বলা হয়।

ফিকের প্রথম সূত্র

ফিকের প্রথম সূত্র ডিফিউসিভ প্রবাহ এবং টেমপ্লেট:Anchor ঘনত্বের গ্রেডিয়েন্টের সম্পর্ক বর্ণনা করে। এটি অনুমান করে যে প্রবাহ উচ্চ ঘনত্বের এলাকা থেকে কম ঘনত্বের এলাকায় যায়, এবং এর মাত্রা ঘনত্বের গ্রেডিয়েন্টের (স্থানিক ডেরিভেটিভ) সাথে আনুপাতিক হয়, বা সহজ ভাষায়, ধারণা হলো যে একটি দ্রবীভূত পদার্থ উচ্চ ঘনত্বের এলাকা থেকে কম ঘনত্বের এলাকায় একটি ঘনত্বের গ্রেডিয়েন্টের মাধ্যমে চলবে। এক (স্থানিক) মাত্রায়, এই সূত্রটি বিভিন্ন আকারে লেখা যেতে পারে, যেখানে সবচেয়ে প্রচলিত আকার (দেখুন) হল মোলার ভিত্তিতে:

$J=-D\frac{d\phi }{dx},$

এখানে

• টেমপ্লেট:Mvar হল ডিফিউশন প্রবাহ, যার মাত্রা হল উপাদান পরিমাণ প্রতি ইউনিট এলাকা প্রতি ইউনিট সময়। টেমপ্লেট:Mvar পরিমাপ করে সেই উপাদান পরিমাণ যা একক সময়ের মধ্যে একক এলাকায় প্রবাহিত হবে,
• টেমপ্লেট:Mvar হল ডিফিউশন সহগ বা ডিফিউসিভিটি। এর মাত্রা হল এলাকা প্রতি ইউনিট সময়,
• $\frac{d\phi }{dx}$ হল ঘনত্ব গ্রেডিয়েন্ট।
• টেমপ্লেট:Mvar (আদর্শ মিশ্রণের জন্য) হল ঘনত্ব, যার মাত্রা হল উপাদান পরিমাণ প্রতি ইউনিট ভলিউম,
• টেমপ্লেট:Mvar হল অবস্থান, যার মাত্রা হল দৈর্ঘ্য।

টেমপ্লেট:Mvar ডিফিউজিং কণার বর্গগতি সাথে আনুপাতিক, যা তাপমাত্রা, ভিসকোসিটি এবং কণার আকারের উপর নির্ভরশীল, যেমন স্টোকস–আয়নস্টাইন সম্পর্ক অনুসারে। সান্দ্র পানির দ্রবীভূত সল্যুশনগুলিতে অধিকাংশ আয়নের ডিফিউশন সহগ সাধারণত একে অপরের কাছাকাছি থাকে এবং ঘরোয়া তাপমাত্রায় এর মান টেমপ্লেট:Val এর মধ্যে থাকে। জীববৈজ্ঞানিক অণুগুলির জন্য ডিফিউশন সহগ সাধারণত ১০^−১০ থেকে ১০^−১১ m²/s-এর মধ্যে থাকে।

দুই বা তার বেশি মাত্রায় আমাদের টেমপ্লেট:Math, ডেল বা গ্রেডিয়েন্ট অপারেটর ব্যবহার করতে হয়, যা প্রথম ডেরিভেটিভের সাধারণীকরণ, এবং আমরা পাই

$𝐉=-D\mathrm{\nabla }\phi ,$

এখানে টেমপ্লেট:Math হল ডিফিউশন প্রবাহ ভেক্টর।

এক-মাত্রিক ডিফিউশনের চালিকা শক্তি হল টেমপ্লেট:Math, যা আদর্শ মিশ্রণের জন্য ঘনত্ব গ্রেডিয়েন্ট।

প্রথম সূত্রের বিভিন্নতা

প্রথম সূত্রের আরেকটি রূপ হলো মূল চলক হিসাবে মাস ভগ্নাংশ (টেমপ্লেট:Mvar, উদাহরণস্বরূপ kg/kg হিসেবে দেওয়া) ব্যবহার করা, তখন সমীকরণটি পরিবর্তিত হয়ে দাঁড়ায়:

${𝐉}_i=-\frac{\rho D}{M_i}\mathrm{\nabla }{y}_i,$

এখানে

• সূচক টেমপ্লেট:Mvar টেমপ্লেট:Mvar^th প্রজাতিকে নির্দেশ করে,
• টেমপ্লেট:Math হল টেমপ্লেট:Mvar^th প্রজাতির ডিফিউশন প্রবাহ ভেক্টর (যেমন mol/m²-s-এ),
• টেমপ্লেট:Math হল টেমপ্লেট:Mvar^th প্রজাতির মোলার ভর,
• টেমপ্লেট:Mvar হল মিশ্রণের ঘনত্ব (যেমন kg/m³).

টেমপ্লেট:Math গ্রেডিয়েন্ট অপারেটরের বাইরে থাকে। এটি কারণ:

$y_i=\frac{{\rho }_{si}}{\rho },$

এখানে টেমপ্লেট:Mvar হল টেমপ্লেট:Mvar^th প্রজাতির আংশিক ঘনত্ব।

এরপর, আদর্শ দ্রবীভূত দ্রবণ বা মিশ্রণ ব্যতীত রাসায়নিক সিস্টেমে, প্রতিটি প্রজাতির ডিফিউশন চালিকা শক্তি হল সেই প্রজাতির রসায়নিক সম্ভাবনার গ্রেডিয়েন্ট। তখন ফিকের প্রথম সূত্র (এক-মাত্রিক ক্ষেত্রে) লেখা যেতে পারে:

$J_i=-\frac{D{c}_i}{RT}\frac{\partial {\mu }_i}{\partial x},$

এখানে

• সূচক টেমপ্লেট:Mvar টেমপ্লেট:Mvar^th প্রজাতিকে নির্দেশ করে,
• টেমপ্লেট:Mvar হল ঘনত্ব (mol/m³),
• টেমপ্লেট:Mvar হল বিশ্বজনীন গ্যাস ধ্রুবক (J/K/mol),
• টেমপ্লেট:Mvar হল পরিপূর্ণ তাপমাত্রা (K),
• টেমপ্লেট:Mvar হল রসায়নিক সম্ভাবনা (J/mol)।

ফিকের সূত্রের চালিকা শক্তি ফুগাসিটি পার্থক্য হিসেবে প্রকাশ করা যেতে পারে:

$J_i=-\frac{D}{RT}\frac{\partial f_i}{\partial x},$

এখানে $f_i$ হল ফুগাসিটি Pa-তে। $f_i$ হল একটি উপাদান টেমপ্লেট:Math-এর আংশিক চাপ, যা বাষ্প $f_i^{\text{G}}$ অথবা তরল $f_i^{\text{L}}$ পর্যায়ে থাকে। বাষ্প-তরল ভারসাম্য অবস্থায় বাষ্পীকরণ প্রবাহ শূন্য হয় কারণ $f_i^{\text{G}}=f_i^{\text{L}}$।

গ্যাসের জন্য ফিকের প্রথম সূত্রের ব্যাখ্যা

দ্বৈত গ্যাস মিশ্রণের জন্য ফিকের সূত্রের চারটি রূপ নীচে দেওয়া হলো। এগুলি ধরে নেয় যে: তাপীয় বিস্তার উপেক্ষাযোগ্য; প্রতি একক ভরের জন্য উভয় প্রজাতির উপর শারীরিক বল সমান; এবং বা চাপ ধ্রুবক, বা উভয় প্রজাতির মোলার ভর সমান। এই শর্তগুলির অধীনে, রেফারেন্স বিস্তারিতভাবে দেখিয়েছে কিভাবে গ্যাসের কাইনেটিক তত্ত্ব থেকে ডিফিউশন সমীকরণটি ফিকের সূত্রের এই রূপে পরিণত হয়: $${𝐕}_{𝐢}=-D\mathrm{\nabla }\ln \left(y_i\right),$$ এখানে টেমপ্লেট:Math হল প্রজাতি টেমপ্লেট:Mvar-এর ডিফিউশন বেগ। প্রজাতির প্রবাহের দৃষ্টিকোণ থেকে এটি হয় $${𝐉}_{𝐢}=-\frac{\rho D}{M_i}\mathrm{\nabla }{y}_i.$$

যদি অতিরিক্তভাবে, $\mathrm{\nabla }\rho =0$, তবে এটি ফিকের সূত্রের সবচেয়ে সাধারণ রূপে পরিণত হয়: $${𝐉}_{𝐢}=-D\mathrm{\nabla }\phi .$$

যদি (অথবা $\mathrm{\nabla }\rho =0$ ছাড়াও) উভয় প্রজাতির মোলার ভর সমান হয়, তবে ফিকের সূত্রটি পরিণত হয় $${𝐉}_{𝐢}=-\frac{\rho D}{M_i}\mathrm{\nabla }{x}_i,$$ এখানে $x_i$ হল প্রজাতি টেমপ্লেট:Mvar-এর মোল অনুপাত।

ফিকের দ্বিতীয় সূত্র

ফিকের দ্বিতীয় সূত্র পূর্বাভাস দেয় কিভাবে ডিফিউশন কনসেনট্রেশনকে সময়ের সাথে পরিবর্তিত করে। এটি একটি আংশিক পার্থক্য সমীকরণ, যা এক-মাত্রিক ক্ষেত্রে এইভাবে লেখা হয়:

$\frac{\partial \phi }{\partial t}=D\frac{{\partial }^2\phi }{\partial x^2},$

এখানে

• টেমপ্লেট:Mvar হল কনসেনট্রেশন, যার মাত্রা $[𝖭{𝖫}^{-3}]$, উদাহরণস্বরূপ mol/m³; টেমপ্লেট:Math হল একটি ফাংশন যা অবস্থান টেমপ্লেট:Mvar এবং সময় টেমপ্লেট:Mvar-এর উপর নির্ভরশীল,
• টেমপ্লেট:Mvar হল সময়, উদাহরণস্বরূপ s,
• টেমপ্লেট:Mvar হল ডিফিউশন কোঅফিশিয়েন্ট, যার মাত্রা $[{𝖫}^2{𝖳}^{-1}]$, উদাহরণস্বরূপ m²/s,
• টেমপ্লেট:Mvar হল অবস্থান, উদাহরণস্বরূপ m।

দ্বৈত বা আরও বেশি মাত্রায় আমরা ল্যাপ্লাসিয়ান টেমপ্লেট:Math ব্যবহার করি, যা দ্বিতীয় ডেরিভেটিভকে সাধারণীকৃত করে, সমীকরণটি প্রাপ্ত হয়:

$\frac{\partial \phi }{\partial t}=D\mathrm{\Delta }\phi .$

ফিকের দ্বিতীয় সূত্রের গাণিতিক রূপ তাপ সমীকরণের মতো এবং এর মৌলিক সমাধান তাপ হিট কের্নেলএর মতো, শুধু তাপ পরিবাহিতা $k$ কে ডিফিউশন কোঅফিশিয়েন্ট $D$ দিয়ে প্রতিস্থাপন করা হয়: $$\phi (x,t)=\frac{1}{\sqrt{4\pi Dt}}\exp (-\frac{x^2}{4Dt}).$$

ফিকের দ্বিতীয় সূত্রের ব্যাখ্যা

ফিকের দ্বিতীয় সূত্র ফিকের প্রথম সূত্র এবং ভর সংরক্ষণ থেকে উৎপন্ন করা যেতে পারে, যদি কোনো রাসায়নিক প্রতিক্রিয়া না ঘটে:

$\frac{\partial \phi }{\partial t}+\frac{\partial }{\partial x}J=0\Rightarrow \frac{\partial \phi }{\partial t}-\frac{\partial }{\partial x}\left(D\frac{\partial }{\partial x}\phi \right)=0.$

যেহেতু ডিফিউশন কোফিশিয়েন্ট টেমপ্লেট:Mvar একটি ধ্রুবক হিসেবে ধরে নেওয়া হয়েছে, এখানে ডিফারেনশিয়েশনের আদান-প্রদান করা যায় এবং ধ্রুবকটি গুণ করা হয়:

$\frac{\partial }{\partial x}\left(D\frac{\partial }{\partial x}\phi \right)=D\frac{\partial }{\partial x}\frac{\partial }{\partial x}\phi =D\frac{{\partial }^2\phi }{\partial x^2},$

এবং, এইভাবে, আমরা ফিকের সূত্রের রূপ পাবো যেটি উপরের মধ্যে উল্লেখ করা হয়েছে।

যখন ডিফিউশন কোফিশিয়েন্ট ধ্রুবক না হয়ে স্থান বা ঘনত্বের উপর নির্ভরশীল হয়, তখন ফিকের দ্বিতীয় সূত্র হয়ে ওঠে:

$\frac{\partial \phi }{\partial t}=D{\mathrm{\nabla }}^2\phi ,$

যা তাপ সমীকরণ এর সাথে সাদৃশ্যপূর্ণ।

যদি ডিফিউশন কোফিশিয়েন্ট একটি ধ্রুবক না হয়ে স্থান বা ঘনত্বের উপর নির্ভরশীল হয়, ফিকের দ্বিতীয় সূত্র হয়ে ওঠে:

$\frac{\partial \phi }{\partial t}=\mathrm{\nabla }\cdot (D\mathrm{\nabla }\phi ).$

একটি গুরুত্বপূর্ণ উদাহরণ হল সেই ক্ষেত্রটি যেখানে টেমপ্লেট:Math একটি স্থির অবস্থায় থাকে, অর্থাৎ ঘনত্ব সময়ের সাথে পরিবর্তিত হয় না, তাহলে উপরের সমীকরণের বাম পাশে শূন্য থাকবে। একমাত্র মাত্রায় স্থির টেমপ্লেট:Mvar এর সাথে ঘনত্বের সমাধান হবে একটি সরলরেখায় ঘনত্বের পরিবর্তন। দুই বা ততোধিক মাত্রায় আমরা পাবো:

${\mathrm{\nabla }}^2\phi =0,$

যা ল্যাপ্লেস সমীকরণ নামে পরিচিত, এবং এর সমাধানগুলো গাণিতিকভাবে হারমনিক ফাংশন হিসেবে পরিচিত।

উদাহরণ সমাধান এবং সাধারণীকরণ

ফিকের দ্বিতীয় সূত্র হল কনভেকশন-ডিফিউশন সমীকরণ এর একটি বিশেষ ক্ষেত্র যেখানে কোনো অ্যাডভেকটিভ ফ্লাক্স এবং কোনো নিট আয়তনিক উৎস নেই। এটি ধারণা সমীকরণ থেকে উৎপন্ন হতে পারে:

$\frac{\partial \phi }{\partial t}+\mathrm{\nabla }\cdot 𝐣=R,$

যেখানে টেমপ্লেট:Math হল মোট ফ্লাক্স এবং টেমপ্লেট:Mvar হল টেমপ্লেট:Math এর জন্য নিট আয়তনিক উৎস। এই পরিস্থিতিতে ফ্লাক্সের একমাত্র উৎস ধরা হয় ডিফিউসিভ ফ্লাক্স:

${𝐣}_{\text{diffusion}}=-D\mathrm{\nabla }\phi .$

ডিফিউসিভ ফ্লাক্সের সংজ্ঞা ধারণা সমীকরণে প্রতিস্থাপন করলে এবং কোন উৎস নেই ধরে (টেমপ্লেট:Math), আমরা ফিকের দ্বিতীয় সূত্রে পৌঁছাই:

$\frac{\partial \phi }{\partial t}=D\frac{{\partial }^2\phi }{\partial x^2}.$

যদি ফ্লাক্স ডিফিউসিভ ফ্লাক্স এবং অ্যাডভেকটিভ ফ্লাক্স উভয়ের ফলস্বরূপ হতো, তবে কনভেকশন-ডিফিউশন সমীকরণ হল ফলস্বরূপ।

উদাহরণ সমাধান ১: স্থির ঘনত্ব উৎস এবং ডিফিউশন দৈর্ঘ্য

একটি সহজ ডিফিউশন কেস সময় টেমপ্লেট:Mvar একমাত্রিকে (যেটি টেমপ্লেট:Mvar-অক্ষ হিসাবে গ্রহণ করা হয়েছে) একটি সীমানা থেকে শুরু হয় যা অবস্থান টেমপ্লেট:Math-এ অবস্থিত, যেখানে ঘনত্ব টেমপ্লেট:Math মানে রাখা হয়েছে তা হলো:

$n(x,t)=n_0\mathrm{erfc}\left(\frac{x}{2\sqrt{Dt}}\right),$

যেখানে টেমপ্লেট:Math হলো পরিপূরক ত্রুটি ফাংশন। এটি সেই কেস যখন ক্ষয়কারী গ্যাসসমূহ অক্সিডেটিভ স্তরের মাধ্যমে ধাতু পৃষ্ঠের দিকে ডিফিউজ হয় (যদি আমরা ধরে নিই যে পরিবেশে গ্যাসের ঘনত্ব স্থির এবং ডিফিউশন স্থান – অর্থাৎ, ক্ষয় পণ্য স্তর – সেমি-অন্তহীন, যা পৃষ্ঠ থেকে শুরু হয়ে উপাদানে অনন্তভাবে বিস্তৃত)। যদি, এর পাল্টা, ডিফিউশন স্থান অন্তহীন হয় (যেখানে টেমপ্লেট:Math, টেমপ্লেট:Math এবং টেমপ্লেট:Math, টেমপ্লেট:Math), তবে সমাধানটি শুধুমাত্র টেমপ্লেট:Sfrac সহ টেমপ্লেট:Math এর সামনে সংশোধিত হয় (যেহেতু এখন ডিফিউশন দুটি দিকে ঘটছে)। এই কেসটি তখন সঠিক যখন কোন সমাধান টেমপ্লেট:Math ঘনত্বের সাথে বিশুদ্ধ দ্রাবক স্তরের সাথে যোগাযোগ করা হয়। (বোকস্টাইন, ২০০৫) দৈর্ঘ্য টেমপ্লেট:Math কে ডিফিউশন দৈর্ঘ্য বলা হয় এবং এটি টেমপ্লেট:Mvar-দিকের মধ্যে ঘনত্ব কিভাবে ডিফিউশনের মাধ্যমে সময় টেমপ্লেট:Mvar এ বিস্তৃত হয়েছে তার একটি পরিমাপ প্রদান করে (বার্ড, ১৯৭৬)।

ত্রুটি ফাংশনের একটি দ্রুত আনুমানিককরণ হিসাবে, টেইলর সিরিজ এর প্রথম দুটি পদ ব্যবহার করা যেতে পারে:

$n(x,t)=n_0[1-2\left(\frac{x}{2\sqrt{Dt\pi }}\right)].$

যদি টেমপ্লেট:Mvar সময়-নির্ভর হয়, তবে ডিফিউশন দৈর্ঘ্য হবে:

$2\sqrt{\underset{0}{\overset{t}{\int }}D(\tau )d\tau }.$

এই ধারণাটি তাপমাত্রার সাথে পরিবর্তিত টেমপ্লেট:Mvar এর জন্য উত্তপ্ত এবং শীতল চক্রের উপর একটি ডিফিউশন দৈর্ঘ্য অনুমান করতে উপকারী।

উদাহরণ সমাধান ২: ব্রাউনিয়ান কণিকা এবং গড় বর্গ স্থানচ্যুতি

আরেকটি সহজ ডিফিউশনের উদাহরণ হলো একটি কণার ব্রাউনিয়ান গতি। কণার প্রাথমিক অবস্থান থেকে এর গড় বর্গ বিচ্যুতি (Mean Squared Displacement - MSD) প্রকাশ করা যায়: $$\text{MSD}\equiv ⟨(𝐱-{𝐱}_{\mathrm{𝟎}}{)}^2⟩=2nDt,$$ যেখানে $n$ হলো কণার ব্রাউনিয়ান গতির মাত্রা। উদাহরণস্বরূপ, একটি কোষঝিল্লির মধ্য দিয়ে ৮ nm পুরু স্তর অতিক্রম করার সময় অণুর ডিফিউশন এক-মাত্রিক (1D) হয় কারণ এটি গোলীয় সাম্যের মধ্যে থাকে। তবে, একটি সুকেন্দ্রিক কোষের কেন্দ্রের দিকে ঝিল্লি থেকে অণুর ডিফিউশন একটি ৩-মাত্রিক (3D) ডিফিউশন। একটি নলাকার ক্যাকটাস এর ক্ষেত্রে, এর পৃষ্ঠের আলোক-সংশ্লেষণকারী কোষ থেকে কেন্দ্রে (এর নলাকার সাম্যের অক্ষ বরাবর) ডিফিউশন একটি ২-মাত্রিক (2D) ডিফিউশন।

গড় বর্গ বিচ্যুতির বর্গমূল $\sqrt{2nDt}$ প্রায়ই কণাটি নির্দিষ্ট সময় $t$ পর কত দূরত্ব অতিক্রম করেছে তা বোঝানোর জন্য ব্যবহৃত হয়। MSD এক-মাত্রিক, দুই-মাত্রিক এবং তিন-মাত্রিক স্থানের উপর সমানভাবে বিতরিত। ফলে, 1D-তে MSD-এর সম্ভাব্যতা বিতরণ গাউসিয়ান এবং 3D-তে এটি একটি ম্যাক্সওয়েল-বোল্টজমান বিতরণ অনুসরণ করে।

সাধারণীকরণ

• অমসৃণ মাধ্যমের ক্ষেত্রে, পরিব্যাপন গুণাঙ্ক স্থানের উপর নির্ভরশীল হয়, টেমপ্লেট:Math। এটি ফিকের প্রথম সূত্রকে পরিবর্তন করে না, কিন্তু দ্বিতীয় সূত্র পরিবর্তিত হয়:

$$\frac{\partial \phi (x,t)}{\partial t}=\mathrm{\nabla }\cdot (D(x)\mathrm{\nabla }\phi (x,t))=D(x)\mathrm{\Delta }\phi (x,t)+\sum _{i=1}^3\frac{\partial D(x)}{\partial x_i}\frac{\partial \phi (x,t)}{\partial x_i}.$$

• অ্যানিসোট্রপিক মাধ্যমে, পরিব্যাপন গুণাঙ্ক দিকের উপর নির্ভরশীল হয়। এটি একটি সিমেট্রিক টেনসর টেমপ্লেট:Math। ফিকের প্রথম সূত্র পরিবর্তিত হয়ে হয়:

$$J=-D\mathrm{\nabla }\phi ,$$

এটি একটি টেনসর ও ভেক্টরের গুণফল:

$$J_i=-\sum _{j=1}^3{D}_{ij}\frac{\partial \phi }{\partial x_j}.$$

ডিফিউশন সমীকরণের জন্য এটি দেয়:

$$\frac{\partial \phi (x,t)}{\partial t}=\mathrm{\nabla }\cdot (D\mathrm{\nabla }\phi (x,t))=\sum _{i=1}^3\sum _{j=1}^3{D}_{ij}\frac{{\partial }^2\phi (x,t)}{\partial x_i\partial x_j}.$$

ডিফিউশন গুণাঙ্কের সিমেট্রিক ম্যাট্রিক্স টেমপ্লেট:Math অবশ্যই পজিটিভ-ডেফিনিট হতে হবে, যাতে ডানদিকের অপারেটর এলিপটিক হয়।

• অমসৃণ অ্যানিসোট্রপিক মাধ্যমের জন্য এই দুই রূপ একত্রিত করে পাওয়া যায়:

$$\frac{\partial \phi (x,t)}{\partial t}=\mathrm{\nabla }\cdot (D(x)\mathrm{\nabla }\phi (x,t))=\sum _{i,j=1}^3(D_{ij}(x)\frac{{\partial }^2\phi (x,t)}{\partial x_i\partial x_j}+\frac{\partial D_{ij}(x)}{\partial x_i}\frac{\partial \phi (x,t)}{\partial x_i}).$$

• আইনস্টাইনের গতিশীলতা এবং টিওরেল সূত্র ভিত্তিক পদ্ধতি ফিকের সমীকরণের জন্য নিম্নলিখিত সাধারণীকরণ প্রদান করে, যা বহু-উপাদান পরিব্যাপনের ক্ষেত্রে প্রযোজ্য:

$$\frac{\partial {\phi }_i}{\partial t}=\sum _j\mathrm{\nabla }\cdot \left(D_{ij}\frac{{\phi }_i}{{\phi }_j}\mathrm{\nabla }{\phi }_j\right),$$

যেখানে টেমপ্লেট:Mvar হল উপাদানগুলির ঘনত্ব এবং টেমপ্লেট:Mvar হল গুণাঙ্কের ম্যাট্রিক্স। এখানে টেমপ্লেট:Mvar এবং টেমপ্লেট:Mvar হল বিভিন্ন উপাদান, স্থানাঙ্ক নয়।

গ্যাসে পরিব্যাপন সম্পর্কিত চ্যাপম্যান–এনস্কগ সূত্র একই রকম পদসমূহ অন্তর্ভুক্ত করে। এই শারীরিক মডেলগুলি পরীক্ষা মডেল টেমপ্লেট:Math থেকে আলাদা, যা শুধুমাত্র সামান্য বিচ্যুতির জন্য বৈধ। পূর্বে, এই রকম পদ ম্যাক্সওয়েল-স্টিফান ব্যাপন সমীকরণে প্রবর্তিত হয়েছিল।

বহু-উপাদান পরিব্যাপনের জন্য অ্যানিসোট্রপিক গুণাঙ্ক নির্ধারণ করতে হলে, একটি চতুর্থ-ক্রমের টেনসর প্রয়োজন, যেমন টেমপ্লেট:Math, যেখানে টেমপ্লেট:Math উপাদান নির্দেশ করে এবং টেমপ্লেট:Math স্থানাঙ্ক নির্দেশ করে।

প্রয়োগসমূহ

ফিকের সূত্রের ভিত্তিতে গঠিত সমীকরণগুলি সাধারণত খাদ্য, নিউরন, বায়োপলিমার, ফার্মাসিউটিক্যালস, ছিদ্রযুক্ত মাটি, জনসংখ্যা গতিবিদ্যা, পারমাণবিক পদার্থ, প্লাজমা পদার্থবিজ্ঞান এবং অর্ধপরিবাহী ডোপিং প্রক্রিয়াগুলির পরিবহন প্রক্রিয়াগুলিকে মডেল করতে ব্যবহৃত হয়। ভোল্টামেট্রি পদ্ধতির তত্ত্ব ফিকের সমীকরণের সমাধানের উপর ভিত্তি করে গঠিত।

অন্যদিকে, কিছু ক্ষেত্রে "ফিকিয়ান" (যা পরিবহন সমীকরণের আরেকটি সাধারণ অনুমান, যা ব্যাপন তত্ত্ব হিসেবে পরিচিত) বর্ণনা পর্যাপ্ত নয়। উদাহরণস্বরূপ, পলিমার বিজ্ঞান এবং খাদ্য বিজ্ঞানে এমন একটি আরও সাধারণ পদ্ধতির প্রয়োজন হয় যা গ্লাস স্থানান্তর অবস্থার মধ্যে থাকা পদার্থের উপাদান পরিবহনকে বর্ণনা করতে পারে।

একটি আরও সাধারণ কাঠামো হলো ম্যাক্সওয়েল-স্টেফান ব্যাপন সমীকরণ যা বহুমাত্রিক ভর পরিবহন মডেল করে। এই সমীকরণ থেকে ফিকের সূত্রকে একটি সীমাবদ্ধ ক্ষেত্রে প্রাপ্ত করা যায়, যখন মিশ্রণটি অত্যন্ত অনুন্নত হয় এবং প্রতিটি রাসায়নিক উপাদান কেবল বাল্ক মিশ্রণের সাথে মিথস্ক্রিয়া করে, অন্য উপাদানের সাথে নয়।

একটি অ-অনুন্নত মিশ্রণে একাধিক উপাদানের উপস্থিতিকে বিবেচনায় নিতে, ম্যাক্সওয়েল-স্টেফান সমীকরণের বিভিন্ন প্রকরণ ব্যবহার করা হয়। এছাড়াও, অ-ক্রান্তিক সংযুক্ত পরিবহন প্রক্রিয়া (ওনসাগার সম্পর্ক) সম্পর্কেও দেখুন।

তরল পদার্থে ফিকের প্রবাহ

যখন দুইটি মিশ্রণযোগ্য তরল একে অপরের সাথে যোগাযোগ করে এবং ব্যাপন ঘটে, তখন ম্যাক্রোস্কোপিক (অথবা গড়) ঘনত্ব ফিকের সূত্র অনুসরণ করে পরিবর্তিত হয়। একটি মেসোস্কোপিক স্কেলে, অর্থাৎ, ম্যাক্রোস্কোপিক স্কেল এবং আণবিক স্কেলের মধ্যে, যেখানে আণবিক এলোমেলো পদক্ষেপ ঘটে, কম্পনগুলোকে উপেক্ষা করা যায় না। এই ধরনের পরিস্থিতিগুলি ল্যান্ডাউ-লিফশিটজ কম্পন হাইড্রোডাইনামিকস দিয়ে সফলভাবে মডেল করা যেতে পারে। এই তাত্ত্বিক কাঠামোতে, ব্যাপন কম্পনগুলির কারণে ঘটে, যার মাত্রা আণবিক স্কেল থেকে ম্যাক্রোস্কোপিক স্কেল পর্যন্ত বিস্তৃত।

বিশেষত, কম্পন হাইড্রোডাইনামিক সমীকরণগুলিতে একটি ফিকের প্রবাহ টার্ম থাকে, একটি নির্দিষ্ট ডিফিউশন সহ, সাথে হাইড্রোডাইনামিক সমীকরণ এবং কম্পন বর্ণনা করা স্তোকাস্টিক টার্ম থাকে। কম্পনগুলি হিসাব করার সময়, একটি প্যারটুরবেটিভ পদ্ধতি ব্যবহার করলে, শূন্য অর্ডার অনুমানটি ফিকের সূত্র হয়। প্রথম অর্ডার অনুমানটি কম্পন প্রদান করে, এবং এটি বেরিয়ে আসে যে কম্পনগুলি ব্যাপনকে অবদান রাখে। এটি কিছুটা যতার্থতা হিসেবে প্রতিফলিত হয়, কারণ নিম্নতর অর্ডার অনুমান দ্বারা বর্ণিত ঘটনা উচ্চতর অনুমানটির ফলস্বরূপ: এই সমস্যা শুধুমাত্র রেনরমালাইজিং করে কম্পন হাইড্রোডাইনামিক সমীকরণগুলি সমাধান করা হয়।

মিশ্রিত দ্রবণের শোষণ গতি এবং সংঘর্ষের ফ্রিকোয়েন্সি

মোলিকুল, কণিকা, এবং পৃষ্ঠগুলির শোষণ, শোষণ, এবং সংঘর্ষ অনেক ক্ষেত্রেই গুরুত্বপূর্ণ সমস্যা। এই মৌলিক প্রক্রিয়াগুলি রসায়ন, জীববিজ্ঞান এবং পরিবেশগত প্রতিক্রিয়া নিয়ন্ত্রণ করে। তাদের হার গণনা করা যায় ব্যাপন ধ্রুবক এবং ফিকের ব্যাপন সূত্র ব্যবহার করে, বিশেষত যখন এই মিথস্ক্রিয়া গলিত দ্রবণে ঘটে।

সাধারণভাবে, ফিকের সূত্র দ্বারা সংজ্ঞায়িত কণিকা এবং মোলিকুলের ব্যাপন ধ্রুবক স্টোকস-আইনস্টাইন সূত্র ব্যবহার করে গণনা করা যেতে পারে। অতিক্ষুদ্র সময়সীমাতে, ব্যাপনের সময়ের আদেশ a²/D, যেখানে a হল কণিকার ব্যাসার্ধ, ব্যাপন ল্যাংভিন সমীকরণ দ্বারা বর্ণিত হয়। দীর্ঘ সময়ের ক্ষেত্রে, ল্যাংভিন সমীকরণ স্টোকস-আইনস্টাইন সূত্র-এ মিশে যায়। এটি গলিত দ্রবণের শর্তে উপযুক্ত, যেখানে দীর্ঘ-পথ ব্যাপন বিবেচনা করা হয়। ল্যাংভিন সমীকরণ ভিত্তিক কম্পন-বিকিরণ থিওরেম অনুসারে, দীর্ঘ সময়ের সীমায় এবং যখন কণিকা তার পরিবেষ্টিত তরল থেকে উল্লেখযোগ্যভাবে ঘন, সময়ের উপর নির্ভরশীল ব্যাপন ধ্রুবক হল:

$D(t)=\mu k_{\mathrm{B}}T(1-e^{-t/(m\mu )}),$

যেখানে (সবকিছু SI এককে)

• k_B হল বোল্টজমান ধ্রুবক,
• T হল সর্বত্র তাপমাত্রা,
• μ হল কণিকার গতি তরল বা গ্যাসে, যা আইনস্টাইন সম্পর্ক (কাইনেটিক তত্ত্ব) ব্যবহার করে গণনা করা যায়,
• m হল কণিকার ভর,
• t হল সময়।

একটি একক মোলিকুল যেমন জৈব মোলিকুল বা জৈব আণুবীক্ষণিক (যেমন প্রোটিন) পানিতে, এক্সপোনেনশিয়াল টার্মটি অবহেলা করা হয় কারণ mμ এর ছোট গুণফল অতিদ্রুত পিকোসেকেন্ড অঞ্চলে খুবই ক্ষুদ্র, সুতরাং এটি তুলনামূলকভাবে ধীর শোষণ প্রক্রিয়ার সাথে সম্পর্কিত নয়।

দ্রাবণে মোলিকুলের ব্যাপন স্কিমা। কমলা দাগগুলি দ্রাব্য মোলিকুল, দ্রাবক মোলিকুলগুলি আঁকা হয়নি, কালো তীর একটি উদাহরণস্বরূপ র‍্যান্ডম ওয়াক ট্রাজেক্টরি, এবং লাল বক্ররেখা হল ফিকের ব্যাপন সূত্রের গাউসিয়ান প্রসারণ সম্ভাবনা ফাংশন।^{:Fig. 9}

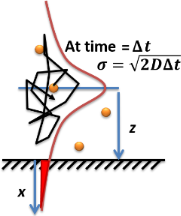
শোষণ বা শোষণ হার একটি গলিত দ্রবণে একটি পাতলাকার দ্রাবক বা তরল-দ্রাবক পৃষ্ঠ বা অভ্যন্তরীণ অংশে শোষিত দ্রাবকের প্রতি গণনা করা যেতে পারে ফিকের ব্যাপন সূত্র ব্যবহার করে। পৃষ্ঠে শোষিত মোলিকুলের একত্রিত সংখ্যা, সময়ের সাথে ব্যাপন প্রবাহ সমীকরণকে একত্রিত করে ল্যাংমুইর-শেফার সমীকরণ দ্বারা প্রকাশ করা হয়, যা এই পৃষ্ঠের প্রথম অংশে সিমুলেটেড মোলিকুলার ব্যাপন দ্বারা প্রদর্শিত হয়েছে:

$\mathrm{\Gamma }=2A{C}_b\sqrt{\frac{Dt}{\pi }}.$

• টেমপ্লেট:Mvar হল পৃষ্ঠের এলাকা (m²).
• $C_b$ হল দ্রাবকের মোলিকুলের সংখ্যা ঘনত্ব (দ্রাব্য) বাল্ক দ্রবণে (#/m³),
• টেমপ্লেট:Mvar হল শোষকের ব্যাপন সহগ (m²/s),
• টেমপ্লেট:Mvar হল অতিবাহিত সময় (s),
• $\mathrm{\Gamma }$ হল একক # মোলিকুল শোষণের সময় $t$ সময়ে একত্রিত মোলিকুলের সংখ্যা।

এই সমীকরণটি আমেরিকান রসায়নবিদ আর্ভিং ল্যাংমুইর এবং ভিনসেন্ট শেফার এর নামানুসারে নামকরণ করা হয়েছে।

সংক্ষেপে, যেমনটি ব্যাখ্যা করা হয়েছে, একটি নতুন তৈরি (t = 0 থেকে) শোষণ পৃষ্ঠ (যেটি $x=0$ এ স্থাপন করা হয়েছে) এর নিকটবর্তী ঘনত্বের প্রোফাইলটি ফিকের সমীকরণ থেকে উপরের অংশে সমাধান করা হয়েছে,

$\frac{\partial C}{\partial x}=\frac{C_b}{\sqrt{\pi Dt}}\text{exp}(-\frac{x^2}{4Dt}),$

যেখানে টেমপ্লেট:Mvar হল $x,t$ এ শোষক মোলিকুলের সংখ্যা ঘনত্ব (#/m³)।

পৃষ্ঠের উপরের অংশে (x = 0) ঘনত্বের গ্রেডিয়েন্টটি বিতরণের প্রি-এক্সপোনেনশিয়াল গুণফলে সরলীকৃত,

${\left(\frac{\partial C}{\partial x}\right)}_{x=0}=\frac{C_b}{\sqrt{\pi Dt}}.$

এবং অঞ্চলে $A.$ এর উপর ব্যাপন (প্রবাহ) হার হল

${\left(\frac{\partial \mathrm{\Gamma }}{\partial t}\right)}_{x=0}=-\frac{DA{C}_b}{\sqrt{\pi Dt}}.$

সময় অনুযায়ী একত্রিত করার সময়,

$\mathrm{\Gamma }=\underset{0}{\overset{t}{\int }}{\left(\frac{\partial \mathrm{\Gamma }}{\partial t}\right)}_{x=0}=2A{C}_b\sqrt{\frac{Dt}{\pi }}.$

ল্যাংমুইর–শেফার সমীকরণটি "পৃষ্ঠ থেকে প্রত্যাখ্যাত মোলিকুলগুলির ব্যাক-ব্যাপন" হিসাব করার জন্য ওয়ার্ড-টোরডাই সমীকরণ-এ প্রসারিত করা যেতে পারে:

$\mathrm{\Gamma }=2A{C}_{\text{b}}\sqrt{\frac{Dt}{\pi }}-A\sqrt{\frac{D}{\pi }}\underset{0}{\overset{\sqrt{t}}{\int }}\frac{C(\tau )}{\sqrt{t-\tau }}d\tau ,$

যেখানে $C_b$ হল বাল্ক কনসেনট্রেশন, $C$ হল সাব-সারফেস কনসেনট্রেশন (যা প্রতিক্রিয়া মডেলের উপর নির্ভর করে সময়ের সাথে পরিবর্তিত হয়), এবং $\tau$ একটি ডামি ভেরিয়েবল।

মন্টে কারলো সিমুলেশনগুলি দেখায় যে এই দুইটি সমীকরণ সেই সিস্টেমগুলির adsorptive হার ভবিষ্যদ্বাণী করতে কাজ করে, যা পৃষ্ঠের নিকটে পূর্বানুমানযোগ্য কনসেনট্রেশন গ্রেডিয়েন্ট তৈরি করে তবে সেই সিস্টেমগুলির জন্য সমস্যায় পড়ে যেগুলিতে কনসেনট্রেশন গ্রেডিয়েন্ট বা অসম্পূর্ণ কনসেনট্রেশন গ্রেডিয়েন্ট থাকে, যেমন typical biosensing সিস্টেম বা যেখানে প্রবাহ এবং কনভেকশন গুরুত্বপূর্ণ।

ডিফিউসিভ শোষণের তত্ত্বগুলির একটি সংক্ষিপ্ত ইতিহাস।

ডিফিউসিভ শোষণের একটি সংক্ষিপ্ত ইতিহাস ডান দিকের ছবিতে দেখানো হয়েছে। একক-মোলিকুল স্তরে ডিফিউসিভ শোষণ বোঝার একটি দৃশ্যমান চ্যালেঞ্জ হল ফ্র্যাক্টাল প্রকৃতি। বেশিরভাগ কম্পিউটার সিমুলেশন ডিফিউশনের জন্য একটি সময় ধাপ নির্বাচন করে যা উপেক্ষা করে যে প্রতিটি ধাপে স্ব-সদৃশ সূক্ষ্ম ডিফিউশন ইভেন্ট (ফ্র্যাক্টাল) রয়েছে। ফ্র্যাক্টাল ডিফিউশন সিমুলেট করলে দেখা যায় যে একটি দুই গুণ সংশোধন প্রবর্তিত হওয়া উচিত, যা একটি স্থির সময় ধাপে শোষণ সিমুলেশন ফলাফলের সাথে সামঞ্জস্যপূর্ণ, যা উপরের দুটি সমীকরণের সাথে মিলে যায়।

উপরের সমীকরণের একটি আরো সমস্যাযুক্ত ফলাফল হল যে এগুলি আদর্শ পরিস্থিতিতে শোষণের নিম্ন সীমা পূর্বানুমান করে তবে বাস্তব শোষণ হার পূর্বানুমান করা খুব কঠিন। সমীকরণগুলি দীর্ঘ সময়ের সীমা শর্তে সংশোধিত হয়েছে যখন একটি স্থিতিশীল কনসেনট্রেশন গ্রেডিয়েন্ট পৃষ্ঠের নিকটে তৈরি হয়েছে। তবে বাস্তব শোষণ প্রায়শই অনেক দ্রুত ঘটে, যেমন এই অনন্ত সময়ের সীমা থেকে, অর্থাৎ, কনসেনট্রেশন গ্রেডিয়েন্ট, সাব-সারফেসে কনসেনট্রেশন হ্রাস, শুধুমাত্র আংশিকভাবে গঠন করা হয় পৃষ্ঠ স্যাচুরেট হওয়ার আগে অথবা প্রবাহ একটি নির্দিষ্ট গ্রেডিয়েন্ট বজায় রাখতে শুরু করার আগে, সুতরাং শোষণের হার প্রায়ই সমীকরণগুলির পূর্বানুমান করা তুলনায় দ্রুত হয়, বিশেষ করে নিম্ন বা কোনও শক্তির বাধা শোষণ (যতক্ষণ না একটি উল্লেখযোগ্য শোষণ শক্তি বাধা না থাকে যা শোষণকে উল্লেখযোগ্যভাবে ধীর করে দেয়), উদাহরণস্বরূপ, পানির-এয়ার বা পানির-সাবস্ট্রেট পৃষ্ঠের একক স্তরের স্বয়ং-অ্যাসেম্বলিতে হাজার থেকে মিলিয়ন গুণ দ্রুত। যেমনটি, এটি প্রয়োজনীয় যে পৃষ্ঠের নিকটবর্তী কনসেনট্রেশন গ্রেডিয়েন্টের বিবর্তন গণনা করা এবং একটি উপযুক্ত সময় বের করা যে সময়ে কাল্পনিক অসীম বিবর্তন বন্ধ করা উচিত বাস্তব প্রয়োগের জন্য। যদিও এটি অনুমান করা কঠিন যে কখন থামানো উচিত, তবে এটি তুলনামূলকভাবে সহজ যে সবচেয়ে কম সময় গণনা করা, সেই সমালোচনামূলক সময় যখন প্রথম নিকটতম প্রতিবেশী সাবস্ট্রেট পৃষ্ঠ থেকে কনসেনট্রেশন গ্রেডিয়েন্টের নির্মাণ অনুভব করতে শুরু করে। এটি শোষণের হার এর সর্বোচ্চ সীমা প্রদান করে আদর্শ পরিস্থিতিতে, যখন শোষক গতিশক্তি ছাড়া কেবলমাত্র ডিফিউশন প্রভাবিত করে:

$⟨r⟩=\frac{4}{\pi }A{C}_b^{4/3}D,$

যেখানে:

• $⟨r⟩$ হল শোষণ হার শক্তির বাধা মুক্ত পরিস্থিতির অধীনে, একক #/s-এ,
• $A$ হল আগ্রহী পৃষ্ঠের এলাকা একটি "অসীম এবং সমতল" সাবস্ট্রেটে (m²),
• $C_b$ হল বাল্ক দ্রবণে শোষক মোলিকুলের কনসেনট্রেশন (#/m³),
• $D$ হল দ্রবণে শোষক (দ্রাবক) এর ডিফিউশন কনস্ট্যান্ট (m²/s), যা ফিকের সূত্র দ্বারা সংজ্ঞায়িত।

এই সমীকরণটি যে কোনো সিস্টেমের প্রাথমিক শোষণ হার পূর্বানুমান করতে ব্যবহৃত হতে পারে; এটি ব্যবহার করা যেতে পারে একটি typical biosensing সিস্টেমের steady-state শোষণ হার পূর্বানুমান করতে যখন বেঁধে রাখার সাইট সাবস্ট্রেট পৃষ্ঠের খুব ছোট অংশ মাত্র, এবং একটি নিকট-পৃষ্ঠ কনসেনট্রেশন গ্রেডিয়েন্ট কখনো তৈরি হয় না; এটি ব্যবহার করা যেতে পারে শোষক মোলিকুলের শোষণ হার পূর্বানুমান করতে পৃষ্ঠের উপর যখন একটি উল্লেখযোগ্য প্রবাহ কনসেনট্রেশন গ্রেডিয়েন্টকে সাব-সারফেসে খুব কমভাবে ঠেলে দেয়।

এই সমালোচনামূলক সময় প্রথম যাত্রী আসার সময় বা গড় মুক্ত-পথ সময় থেকে উল্লেখযোগ্যভাবে আলাদা। গড় প্রথম-যাত্রী সময় এবং ফিকের ডিফিউশন সূত্র ব্যবহার করে গড় বেঁধে যাওয়ার হার অনুমান করা কনসেনট্রেশন গ্রেডিয়েন্টকে অতিরিক্ত ভাবে অনুমান করবে কারণ প্রথম যাত্রী সাধারণত অনেক স্তরের প্রতিবেশী থেকে আসে, ফলে তার আসার সময় প্রথম প্রতিবেশী ডিফিউশন সময়ের তুলনায় অনেক বেশি হবে। গড় মুক্ত পথ সময় এবং ল্যাংমুইর সমীকরণ ব্যবহার করা একটি কৃত্রিম কনসেনট্রেশন গ্রেডিয়েন্ট তৈরি করবে প্রথম যাত্রীর প্রাথমিক অবস্থান এবং লক্ষ্য পৃষ্ঠের মধ্যে, কারণ অন্য প্রতিবেশী স্তরগুলির এখনও কোনও পরিবর্তন হয়নি, ফলে প্রকৃত শোষণ সময়কে উল্লেখযোগ্যভাবে কম অনুমান করবে, অর্থাৎ, প্রকৃত প্রথম যাত্রী আসার সময় নিজেই, উপরের হারের বিপরীত, গণনা করা কঠিন। যদি সিস্টেমটি 1D ডিফিউশন হিসেবে সহজ করা যায়, তবে গড় প্রথম যাত্রী সময় হিসাব করা যেতে পারে একই নিকটতম প্রতিবেশী সমালোচনামূলক ডিফিউশন সময় ব্যবহার করে প্রথম প্রতিবেশী দূরত্ব হতে MSD,

$L=\sqrt{2Dt},$

যেখানে:

• $L=C_b^{-1/3}$ (একক m) হল গড় নিকটতম প্রতিবেশী দূরত্ব, যা ঘন প্যাকিং হিসেবে আনুমানিক, যেখানে $C_b$ হল বাল্ক দ্রবণে দ্রাবকের কনসেনট্রেশন (একক # মোলিকুল / m³),
• $D$ হল ডিফিউশন কনস্ট্যান্ট যা ফিকের সমীকরণ দ্বারা সংজ্ঞায়িত (একক m²/s),
• $t$ হল সমালোচনামূলক সময় (একক s)。

এই সমালোচনামূলক সময়ে, প্রথম যাত্রীর আসা এবং শোষিত হওয়া সম্ভব নয়। তবে এটি প্রতিবেশী স্তরের আগমনের গতি সেট করে। এই গতির সাথে, যেখানে কনসেনট্রেশন গ্রেডিয়েন্ট প্রথম প্রতিবেশী স্তরের চারপাশে থেমে যায়, গ্রেডিয়েন্ট আরও সময় ধরে প্রকৃত প্রথম যাত্রীর আগমনের সময়ে প্রকৃতপক্ষে বিস্তার লাভ করে না। এই গতিতে, একটি 1D সমস্যায় 3D ডিফিউসিভ শোষণ সমস্যা রূপান্তরিত করার জন্য একাধিক প্যাকিং অনুমান এবং অন্যান্য প্রতিবেশী উপেক্ষা করা হলে সমাধানটি হালকা পার্থক্য সহ মিলিত হতে পারে।

যখন আগ্রহের ক্ষেত্রটি একটি অণুর আকারের (বিশেষত, একটি দীর্ঘ সিলিন্ড্রিক অণু যেমন DNA) সমান হয়, তখন শোষণ হার সমীকরণটি দুটি অণুর সংঘর্ষের ফ্রিকোয়েন্সি প্রতিনিধিত্ব করে যা একটি সান্দ্রিত দ্রবণে রয়েছে, যেখানে একটি অণু একটি নির্দিষ্ট পাশ রয়েছে এবং অন্যটি কোন স্টেরিক নির্ভরতা নেই, অর্থাৎ, একটি অণু (এমনকি এলোমেলো অভ্যন্তরীণ অবস্থা) অন্যটির একটি পাশের সাথে সংযোগ স্থাপন করে। ডিফিউশন ধ্রুবকটি আপডেট করতে হবে দুইটি ডিফিউজিং অণুর মধ্যে আপেক্ষিক ডিফিউশন ধ্রুবক হিসেবে। এই অনুমানটি বিশেষভাবে একটি ছোট অণু এবং একটি বড় অণুর মধ্যে মিথস্ক্রিয়া অধ্যয়ন করতে উপকারী, যেমন একটি প্রোটিন। কার্যকর ডিফিউশন ধ্রুবকটি ছোট অণুর দ্বারা আধিপত্য করা হয়, যার ডিফিউশন ধ্রুবকটি পরিবর্তে ব্যবহার করা যেতে পারে।

উপরের সংঘর্ষ হার সমীকরণটি একটি পৃষ্ঠের উপর আণবিক স্ব-সংগঠন এর গতিশক্তি পূর্বাভাস করতে সহায়ক। অণুগুলি সলিউশনটি র্যান্ডমভাবে অভ্যন্তরীণভাবে থাকে। ধরে নেওয়া হচ্ছে ১/৬ অংশ অণুর সঠিক অভ্যন্তরীণ অবস্থান রয়েছে পৃষ্ঠের বাইন্ডিং সাইটগুলির সাথে, অর্থাৎ x, y, z তিনটি মাত্রার মধ্যে z-দিকের ১/২, সুতরাং আগ্রহের কনসেন্ট্রেশনটি কেবল ১/৬ সলিউশনের মোট কনসেন্ট্রেশন। এই মানটি সমীকরণে দিয়ে, ল্যাংমুইর শোষণ মডেল ব্যবহার করে তাত্ত্বিক শোষণ গতিশক্তি তলিকা করতে সক্ষম হওয়া উচিত। আরও শক্তিশালী চিত্রে, ১/৬ অংশটি বাইন্ডিং জ্যামিতির স্টেরিক ফ্যাক্টর দ্বারা প্রতিস্থাপিত হতে পারে।

সংঘর্ষ তত্ত্ব এবং ডিফিউসিভ সংঘর্ষ তত্ত্বের তুলনা।

বাইমোলিকুলার সংঘর্ষ ফ্রিকোয়েন্সি অনেক প্রতিক্রিয়া সম্পর্কিত, যার মধ্যে প্রোটিন কোঅ্যাগুলেশন/অ্যাগ্রিগেশন শুরুতে স্মোলুচোস্কি কোঅ্যাগুলেশন সমীকরণ দ্বারা বর্ণিত হয়েছে, যা মারিয়ান স্মোলুচোস্কি ১৯১৬ সালে একটি গুরুত্বপূর্ণ প্রকাশনায় প্রস্তাব করেছিলেন, যা ব্রাউনিয়ান গতিবিধি এবং ফিকের ব্যাপন সূত্রগুলির দ্বারা উদ্ভূত। একটি আদর্শ প্রতিক্রিয়া শর্তে A + B → পণ্য একটি সান্দ্রিত দ্রবণে, স্মোলুচোস্কি পরামর্শ দিয়েছিলেন যে অণুর ফ্লাক্স সীমাহীন সময়ের সীমাতে হিসাব করা যেতে পারে ফিকের ব্যাপন সূত্র থেকে, যা লক্ষ্য অণুর একটি নির্দিষ্ট/স্থিতিশীল কনসেন্ট্রেশন গ্র্যাডিয়েন্ট দেয়, যেমন B লক্ষ্য অণু হিসেবেই স্থির থাকে, এবং A চলমান অণু যা A এবং B-এর মধ্যে কোঅ্যাগুলেশন প্রতিক্রিয়া সৃষ্টি করে B লক্ষ্য অণুর কাছে কনসেন্ট্রেশন গ্র্যাডিয়েন্ট তৈরি করে। স্মোলুচোস্কি সমীকরণের মাধ্যমে A এবং B-এর মধ্যে সংঘর্ষ ফ্রিকোয়েন্সি হিসাব করেছিলেন একক #/s/m³ হিসেবে:

$Z_{AB}=4\pi R{D}_r{C}_A{C}_B,$

যেখানে:

• $R$ হচ্ছে সংঘর্ষের ব্যাসার্ধ,
• $D_r=D_A+D_B$ হচ্ছে A এবং B-এর মধ্যে আপেক্ষিক ডিফিউশন ধ্রুবক (m²/s),
• $C_A$ এবং $C_B$ হচ্ছে যথাক্রমে A এবং B-এর সংখ্যা কনসেন্ট্রেশন (#/m³)।

এই বাইমোলিকুলার প্রতিক্রিয়া শর্তের রিঅ্যাকশন অর্ডার ২, যা সংঘর্ষ তত্ত্ব থেকে আনা ফলাফলটি প্রতিস্থাপন করে অণুর চলমান গতির সাথে ডিফিউশন ফ্লাক্স। সংঘর্ষ তত্ত্বে, A এবং B-এর মধ্যে ভ্রমণ সময় দূরত্বের সাথে অনুপাতিক, যা ডিফিউশন কেসের জন্য একটি অনুরূপ সম্পর্ক যদি ফ্লাক্স স্থির থাকে।

তবে, একটি ব্যবহারিক শর্তে, লক্ষ্য অণুর কাছাকাছি কনসেন্ট্রেশন গ্র্যাডিয়েন্ট সময়ের সাথে পরিবর্তিত হয় এবং অণুর ফ্লাক্সও পরিবর্তিত হয়, এবং গড়ে ফ্লাক্স স্মোলুচোস্কির প্রস্তাবিত সীমাহীন সময় সীমার চেয়ে অনেক বড়। প্রথম যাত্রী আগমনের সময়ের আগে, ফিকের সমীকরণ সময়ের সাথে কনসেন্ট্রেশন গ্র্যাডিয়েন্ট পূর্বাভাস দেয় যা বাস্তবে এখনও তৈরি হয়নি। সুতরাং, এই স্মোলুচোস্কি ফ্রিকোয়েন্সি আসল সংঘর্ষ ফ্রিকোয়েন্সির নিম্ন সীমানা প্রতিনিধিত্ব করে।

২০২২ সালে, চেন A এবং B-এর মধ্যে সংঘর্ষ ফ্রিকোয়েন্সির উপরের সীমা হিসাব করেছিলেন, ধরে নিয়ে যে চলমান অণুর বাল্ক কনসেন্ট্রেশন প্রথম লক্ষণীয় প্রতিবেশী অণুর পরে স্থির থাকে। সুতরাং কনসেন্ট্রেশন গ্র্যাডিয়েন্টের বিবর্তন প্রথম প্রতিবেশী স্তরে থেমে যায় এবং একটি স্টপ-টাইমের মাধ্যমে প্রকৃত ফ্লাক্স হিসাব করা হয়। তিনি এটিকে 'সাংঘাতিক সময়' বলে অভিহিত করেছেন এবং একক #/s/m³ এ ডিফিউসিভ সংঘর্ষ ফ্রিকোয়েন্সি প্রাপ্ত করেছেন:

$Z_{AB}=\frac{8}{\pi }\sigma D_r{C}_A{C}_B\sqrt[3]{C_A+C_B},$

যেখানে:

• $\sigma$ হচ্ছে সংঘর্ষের ক্রস-সেকশনের এলাকা (m²),
• $D_r=D_A+D_B$ হচ্ছে A এবং B-এর মধ্যে আপেক্ষিক ডিফিউশন ধ্রুবক (m²/s),
• $C_A$ এবং $C_B$ হচ্ছে যথাক্রমে A এবং B-এর সংখ্যা কনসেন্ট্রেশন (#/m³),
• $\sqrt[3]{C_A+C_B}$ প্রতিনিধিত্ব করে 1/<d>, যেখানে d হচ্ছে দুইটি অণুর গড় দূরত্ব।

এই সমীকরণটি ধারণা করে যে A এবং B-এর মধ্যে একটি ডিফিউসিভ সংঘর্ষ ফ্রিকোয়েন্সির উপরের সীমা হল যখন প্রথম প্রতিবেশী স্তর কনসেন্ট্রেশন গ্র্যাডিয়েন্টের বিবর্তন অনুভব করতে শুরু করে, যার প্রতিক্রিয়া অর্ডার টেমপ্লেট:Sfrac পরিবর্তে ২। উভয় স্মোলুচোস্কি সমীকরণ এবং চেন সমীকরণ আয়তন পরীক্ষা সঠিক SI এককগুলি মেনে চলে। তবে প্রথমটি ব্যাসার্ধের উপর নির্ভরশীল এবং দ্বিতীয়টি সংঘর্ষ বলয়ের ক্ষেত্রের উপর নির্ভরশীল। মাত্রিক বিশ্লেষণ থেকে, সংঘর্ষ বলয়ের আয়তনের উপর নির্ভরশীল একটি সমীকরণ থাকবে, তবে সব সমীকরণই শেষ পর্যন্ত একই সংখ্যাগত সংঘর্ষ হার পরিণত হবে যা পরীক্ষামূলকভাবে পরিমাপ করা যায়। একটি বাইমোলিকুলার একক প্রতিক্রিয়ার প্রকৃত রিঅ্যাকশন অর্ডার ২ এবং টেমপ্লেট:Sfrac এর মধ্যে হতে পারে, যা যুক্তিসঙ্গত কারণ ডিফিউসিভ সংঘর্ষ সময় সম্পূর্ণরূপে দুইটি অণুর মধ্যে দূরত্বের উপর নির্ভরশীল।

এই নতুন সমীকরণগুলি শোষণ হার সমীকরণের শূন্য সময়ের এককতারতা এড়িয়ে চলে ল্যাংমুইর-শেফার সমীকরণের জন্য। আদর্শ শর্তে অমুক দুটি অণু একে অপরকে দ্রবণে বা বিপরীতভাবে মন্ত্রমুগ্ধভাবে উপস্থাপন করলে তাদের একে অপরকে অতিক্রম করার সম্ভাবনা সর্বদা শূন্য সময়ে থাকে, অতএব সেই দুইটি অণুর সংযুক্তির হার শূন্য সময়ে অনন্ত হবে। তা যদি না হয় যে অন্যান্য কোটি কোটি অণু তাদের প্রথম সঙ্গী পেতে অপেক্ষা করতে হবে। গড়ে, এই হার তাই অনন্ত হবে। কিন্তু পরিসংখ্যানিকভাবে এই যুক্তি অর্থহীন। শূন্য সময়ের মধ্যে একটি অণুর সর্বোচ্চ হার ১, একে অপরকে মিলিত করা না হয়, তাই শূন্য সময়ে ওই অণু যুগলটির অনন্ত হার আসলে এক হওয়া উচিত, যা গড়ে ১/কোটি বা আরও পরিসংখ্যানিকভাবে উপেক্ষাযোগ্য। বাস্তবে দুটি অণু শূন্য সময়ে একে অপরকে একযোগভাবে দেখা করতে পারে না।

জৈবিক দৃষ্টিকোণ

প্রথম সূত্রটি নিম্নলিখিত সূত্রের সৃষ্টি করে:

$\text{flux}=-P(c_2-c_1),$

যেখানে

• টেমপ্লেট:Mvar হলো পারমিয়েবিলিটি, একটি পরীক্ষামূলকভাবে নির্ধারিত ঝিল্লির "সঞ্চালন" নির্দিষ্ট গ্যাসের জন্য এবং নির্দিষ্ট তাপমাত্রায়,
• টেমপ্লেট:Math হলো গ্যাসের ঘনত্ব পার্শ্ববর্তী ঝিল্লি এর মাধ্যমে প্রবাহের দিক অনুযায়ী (টেমপ্লেট:Math থেকে টেমপ্লেট:Math)।

ফিকের প্রথম সূত্রটি রেডিয়েশন স্থানান্তরের সমীকরণগুলিতেও গুরুত্বপূর্ণ। তবে, এই প্রসঙ্গে, এটি তখনই অযথাযথ হয়ে যায় যখন ব্যাপন ধ্রুবক কম থাকে এবং রেডিয়েশন আলোচনার গতি দ্বারা সীমাবদ্ধ হয়, গ্যাসের পরিবর্তে পদার্থের প্রতিরোধের কারণে। এই পরিস্থিতিতে, ফ্লাক্স লিমিটার ব্যবহার করা যেতে পারে।

গ্যাসের একটি তরল ঝিল্লির মাধ্যমে এক্সচেঞ্জ রেট এই সূত্রের সাথে গ্রাহামের সূত্র ব্যবহার করে নির্ধারণ করা যেতে পারে।

একটি পাতলা দ্রবণের অবস্থায় যখন ব্যাপন নিয়ন্ত্রণ নেয়, তখন উপরের বিভাগে উল্লেখিত ঝিল্লি পারমিয়েবিলিটি সূত্রটি দ্রব্যের জন্য তাত্ত্বিকভাবে হিসাব করা যেতে পারে, যা গত অধ্যায়ে উল্লিখিত সূত্র ব্যবহার করা যেতে পারে (বিশেষ যত্ন সহকারে ব্যবহার করুন কারণ সূত্রটি ঘন দ্রব্যের জন্য উৎপন্ন, যখন জীববৈজ্ঞানিক অণুগুলি পানি অপেক্ষা ঘন নয়। এছাড়া, এই সূত্রটি ঝিল্লির কাছাকাছি আদর্শ ঘনত্বের অগ্রাধিকার সূচনা এবং বিকাশের ধারণা করে):

$P=2A_p{\eta }_{tm}\sqrt{\frac{D}{\pi t}},$

যেখানে:

• $A_P$ হলো ঝিল্লির উপর ছিদ্রের মোট এলাকা (একক m²),
• ${\eta }_{tm}$ হলো ট্রান্সমেমব্রেন দক্ষতা (এককবিহীন), যা ক্রোমাটোগ্রাফি এর গতিশীল তত্ত্ব থেকে হিসাব করা যেতে পারে,
• D হলো দ্রব্যের ব্যাপন ধ্রুবক (একক m²⋅s⁻¹),
• t হলো সময় (একক s),
• c₂, c₁ ঘনত্বকে mol m⁻³ এককে ব্যবহার করতে হবে, ফলে ফ্লাক্সের একক হবে mol s⁻¹।

ফ্লাক্স সময়ের বর্গমূলের সাথে কমে যায় কারণ ঝিল্লির কাছে ঘনত্বের গ্রেডিয়েন্ট সময়ের সাথে তৈরি হয় আদর্শ অবস্থায়। যখন প্রবাহ এবং কনভেকশন থাকে, তখন ফ্লাক্সটি উল্লেখযোগ্যভাবে ভিন্ন হতে পারে এবং এটি একটি স্থির সময় t প্রদর্শন করতে পারে, যা ফ্লাক্সকে স্থির করে তুলতে পারে, সময়ের সাথে কমে যাওয়ার পরিবর্তে। একটি সমালোচনামূলক সময় আদর্শ প্রবাহ পরিস্থিতিতে অনুমান করা হয়েছে, যখন কোন গ্রেডিয়েন্ট গঠন হয়নি। এই কৌশলটি জীববিজ্ঞানে যেমন রক্ত সঞ্চালন ব্যবহৃত হয়।

সেমিকন্ডাক্টর উৎপাদনে প্রয়োগ

সেমিকন্ডাক্টর হল ডিভাইসগুলির একটি সমষ্টিগত পরিভাষা। এটি মূলত তিনটি শ্রেণিতে বিভক্ত: দুই টার্মিনাল ডিভাইস, তিন টার্মিনাল ডিভাইস, এবং চার টার্মিনাল ডিভাইস। সেমিকন্ডাক্টরের সংমিশ্রণকে সমন্বিত পরিসর (ইন্টিগ্রেটেড সার্কিট) বলা হয়।

ফিকের সূত্র এবং সেমিকন্ডাক্টরের সম্পর্ক: সেমিকন্ডাক্টরের মূলনীতি হল একটি স্তর থেকে অন্য স্তরে রাসায়নিক বা ডোপ্যান্ট স্থানান্তর করা। ফিকের সূত্র ব্যবহার করে ডোপ্যান্ট বা রাসায়নিকগুলির গতি প্রতি মিটার এবং প্রতি সেকেন্ডে কতটা হওয়া উচিত তা গণনা করে ডিফিউশন নিয়ন্ত্রণ এবং পূর্বাভাস দেওয়া সম্ভব।

অতএব, বিভিন্ন প্রকার এবং স্তরের সেমিকন্ডাক্টর প্রস্তুত করা সম্ভব।

ইন্টিগ্রেটেড সার্কিট প্রস্তুতি প্রযুক্তি, মডেল প্রক্রিয়া যেমন CVD, তাপ অক্সিডেশন, ভেজা অক্সিডেশন, ডোপিং ইত্যাদি ফিকের সূত্র থেকে প্রাপ্ত ডিফিউশন সমীকরণ ব্যবহার করে।

CVD পদ্ধতিতে সেমিকন্ডাক্টর তৈরি

ওয়েফার একটি ধরনের সেমিকন্ডাক্টর, যার সিলিকন সাবস্ট্রেটের উপরে একটি CVD-সৃষ্টি পলিমার চেইন এবং ফিল্মের স্তর প্রলেপিত থাকে। এই ফিল্মে এন-টাইপ এবং পি-টাইপ ডোপ্যান্ট থাকে এবং ডোপ্যান্ট পরিবহণের জন্য দায়ী। CVD এর মূলনীতি হল গ্যাস-ফেজ এবং গ্যাস-সলিড রাসায়নিক প্রতিক্রিয়া মাধ্যমে পাতলা ফিল্ম তৈরি করা।

CVD-এ ঘনত্ব প্রবাহ শাসিত হয় চাপের গ্রেডিয়েন্ট দ্বারা। CVD তে একটি ডিফিউশন উপাদানও রয়েছে, যা অ্যাডাটমের পৃষ্ঠীয় ডিফিউশন থেকে পৃথক। CVD-তে প্রতিক্রিয়া এবং উৎপাদনকে সাবস্ট্রেটের পাশে একটি স্থির গ্যাসের সীমানা স্তর মাধ্যমে ডিফিউজ করতে হবে। CVD ফিল্ম বৃদ্ধির জন্য মোট পদক্ষেপগুলির মধ্যে গ্যাস-ফেজ ডিফিউশন, অ্যাডাটমের শোষণ এবং পৃষ্ঠীয় ডিফিউশন, সাবস্ট্রেটের উপর প্রতিক্রিয়া এবং গ্যাস-ফেজে উৎপাদনের ডিফিউশন অন্তর্ভুক্ত রয়েছে।

গ্যাস প্রবাহের গতির প্রোফাইল হল: $$\delta (x)=\left(\frac{5x}{{\mathrm{R}\mathrm{e}}^{1/2}}\right)\mathrm{R}\mathrm{e}=\frac{v\rho L}{\eta },$$ যেখানে:

• $\delta$ হল বেধ,
• $\mathrm{R}\mathrm{e}$ হল রেইনল্ডস সংখ্যা,
• টেমপ্লেট:Mvar হল সাবস্ট্রেটের দৈর্ঘ্য,
• টেমপ্লেট:Math যে কোনও পৃষ্ঠে,
• $\eta$ হল ভিসকোসিটি,
• $\rho$ হল ঘনত্ব।

টেমপ্লেট:Mvar কে টেমপ্লেট:Math থেকে টেমপ্লেট:Mvar পর্যন্ত একত্রিত করলে, এটি গড় বেধ দেয়: $$\delta =\frac{10L}{3{\mathrm{R}\mathrm{e}}^{1/2}}.$$

প্রতিক্রিয়া ব্যালেন্স রাখতে, প্রতিক্রিয়া গ্যাসের সীমানা স্তর মাধ্যমে সাবস্ট্রেটের কাছে পৌঁছানোর জন্য ডিফিউজ করতে হবে। তাই একটি পাতলা সীমানা স্তর কাম্য। সমীকরণের মতে, ভিও বাড়ালে আরও প্রতিক্রিয়া গ্যাসের অপচয় হবে। প্রবাহ যদি অস্থির হয়ে যায়, তবে প্রতিক্রিয়া গ্যাসটি সাবস্ট্রেটের উপর একরূপভাবে পৌঁছাবে না। আরেকটি অপশন হল কম ভিসকোসিটি বা কম ঘনত্বের একটি নতুন ক্যারিয়ার গ্যাস ব্যবহার করা।

ফিকের প্রথম সূত্র সীমানা স্তরের মাধ্যমে ডিফিউশন বর্ণনা করে। একটি গ্যাসের চাপ (p) এবং তাপমাত্রা (T) এর ফাংশন হিসেবে ডিফিউশন নির্ধারিত হয়।

$$D=D_0\left(\frac{p_0}{p}\right){\left(\frac{T}{T_0}\right)}^{3/2},$$ যেখানে:

• $p_0$ হল মানক চাপ,
• $T_0$ হল মানক তাপমাত্রা,
• $D_0$ হল মানক ডিফিউসিভিটি।

এই সমীকরণটি বলে যে তাপমাত্রা বাড়ানো বা চাপ কমানো ডিফিউসিভিটিকে বাড়াতে পারে।

ফিকের প্রথম সূত্র প্রতিক্রিয়া গ্যাসের সাবস্ট্রেটে প্রবাহ এবং সাবস্ট্রেট থেকে উৎপাদনের জন্য প্রবাহের পূর্বাভাস দেয়: $$J=-D_i\left(\frac{d{c}_i}{dx}\right),$$ যেখানে:

• $x$ হল বেধ $\delta$,
• $d{c}_i$ হল প্রথম প্রতিক্রিয়া গ্যাসের কনসেনট্রেশন।

আইডিয়াল গ্যাস সূত্র $pV=nRT$ অনুসারে, গ্যাসের কনসেনট্রেশন আংশিক চাপ দ্বারা প্রকাশিত হয়।

$$J=-D_i\left(\frac{p_i-p_0}{\delta RT}\right),$$ যেখানে:

• $R$ হল গ্যাস কনস্ট্যান্ট,
• $\frac{p_i-p_0}{\delta }$ হল আংশিক চাপ গ্রেডিয়েন্ট।

ফলে, ফিকের প্রথম সূত্র আমাদের বলে দেয় যে আমরা একটি আংশিক চাপ গ্রেডিয়েন্ট ব্যবহার করে ডিফিউসিভিটি নিয়ন্ত্রণ করতে এবং সেমিকন্ডাক্টরের পাতলা ফিল্মগুলির বৃদ্ধির নিয়ন্ত্রণ করতে পারি।

অনেক বাস্তব পরিস্থিতিতে, সহজ ফিকের সূত্র সেমিকন্ডাক্টরের সমস্যার জন্য একটি পর্যাপ্ত সূত্র নয়। এটি কেবল নির্দিষ্ট শর্তে প্রযোজ্য, যেমন সেমিকন্ডাক্টরের সীমানা শর্ত: ধ্রুবক উৎস কনসেনট্রেশন ডিফিউশন, সীমিত উৎস কনসেনট্রেশন, অথবা চলন্ত সীমানা ডিফিউশন।

ফিকিয়ান ব্যাপনের অবৈধতা

যদিও ফিকিয়ান ব্যাপনকে প্রাথমিক দিনগুলিতে সেমিকন্ডাক্টর উৎপাদন প্রক্রিয়া (যেমন সিভিডি রিএকটর) মডেল করতে ব্যবহার করা হয়েছে, তবে এটি প্রায়ই উন্নত সেমিকন্ডাক্টর নোড (< ৯০ nm) এ ব্যাপন প্রক্রিয়া সঠিকভাবে মডেল করতে ব্যর্থ হয়। এটি মূলত ফিকিয়ান ব্যাপনের অক্ষমতা থেকে উদ্ভূত যা আণবিক স্তরে এবং তার নিচে ব্যাপন প্রক্রিয়া সঠিকভাবে মডেল করতে পারে না। উন্নত সেমিকন্ডাক্টর উৎপাদনে, আণবিক স্তরে গতিবিধি বোঝা গুরুত্বপূর্ণ, যা কন্টিনিউম ব্যাপন দ্বারা ব্যর্থ হয়। আজকাল, বেশিরভাগ সেমিকন্ডাক্টর নির্মাতা রেন্ডম ওয়াক ব্যবহার করে ব্যাপন প্রক্রিয়া অধ্যয়ন এবং মডেল করার জন্য। এটি আমাদের একক পরমাণু, অণু, প্লাজমা ইত্যাদির গতিবিধি বোঝার জন্য ব্যাপন প্রক্রিয়া ডিসক্রিট পদ্ধতিতে অধ্যয়ন করতে সহায়তা করে।

এমন একটি প্রক্রিয়াতে, ব্যাপনকারী প্রজাতির (পরমাণু, অণু, প্লাজমা ইত্যাদি) গতিবিধিকে একটি ডিসক্রিট সত্তা হিসেবে বিবেচনা করা হয়, যা সিভিডি রিএকটর, সীমানা স্তর, উপাদান কাঠামো ইত্যাদির মধ্য দিয়ে র্যান্ডম ওয়াক অনুসরণ করে। কখনও কখনও, প্রক্রিয়া শর্তের উপর নির্ভর করে গতিবিধি একটি পক্ষপাতি র্যান্ডম ওয়াক অনুসরণ করতে পারে। পরিসংখ্যানিক বিশ্লেষণ করা হয় যাতে প্রজাতির র্যান্ডম ওয়াক থেকে উদ্ভূত পরিবর্তন/স্টোকাস্টিসিটি বোঝা যায়, যা পরবর্তীতে সামগ্রিক প্রক্রিয়া এবং বৈদ্যুতিন পরিবর্তনকে প্রভাবিত করে।

খাদ্য উৎপাদন এবং রান্না

ফিকের প্রথম সূত্রের সূত্রটি খাদ্য এবং রান্নার প্রেক্ষাপটে বিভিন্ন জটিল ঘটনা ব্যাখ্যা করতে পারে: যেমন, ইথিলিনের মতো অণুর ব্যাপন উদ্ভিদ বৃদ্ধির এবং পাকার প্রক্রিয়া উৎসাহিত করে, লবণ এবং চিনি অণু মাংসের প্রক্রিয়াকরণ ও ম্যারিনেটিংয়ে সহায়ক হয়, এবং পানি অণু ডিহাইড্রেশনকে উৎসাহিত করে। ফিকের প্রথম সূত্রটি রান্নার সময় স্প্যাগেটি নুডলের মধ্যে জল শোষণের সময় পরিবর্তনশীল আর্দ্রতা প্রোফাইল পূর্বাভাস দেওয়ার জন্যও ব্যবহার করা যেতে পারে। এই সমস্ত ঘটনা হলো দ্রাব্য কণাগুলির স্বতঃস্ফূর্ত গমন, যা ঘনত্বের পার্থক্য দ্বারা চালিত। বিভিন্ন পরিস্থিতিতে, আলাদা আলাদা ডিফিউজিভিটি থাকে যা একটি ধ্রুবক।

ঘনত্বের পার্থক্য নিয়ন্ত্রণ করে, রান্নার সময়, খাদ্যের আকার এবং লবণ দেয়া নিয়ন্ত্রণ করা যায়।

আরও দেখুন

• অ্যাডভেকশন
• চার্চিল–বার্নস্টেইন সমীকরণ
• ব্যাপন
• ফেলস ব্যাপন
• গ্যাস বিনিময়
• ভর প্রবাহ
• ম্যাক্সওয়েল–স্টেফান ব্যাপন
• নেরস্ট–প্লাঙ্ক সমীকরণ
• অভিস্রবণ

আরও পড়ুন

• টেমপ্লেট:বই উদ্ধৃতি
• টেমপ্লেট:বই উদ্ধৃতি
• টেমপ্লেট:বই উদ্ধৃতি
• টেমপ্লেট:বই উদ্ধৃতি
• টেমপ্লেট:সাময়িকী উদ্ধৃতি – পুনর্মুদ্রিত টেমপ্লেট:সাময়িকী উদ্ধৃতি
• টেমপ্লেট:বই উদ্ধৃতি

বহিঃসংযোগ

• ফিকের সমীকরণ, বল্টসম্যানের রূপান্তর ইত্যাদি (চিত্র এবং অ্যানিমেশন সহ)
• ফিকের দ্বিতীয় সূত্র OpenStax