ডোমেইন রঞ্জন

ডোমেইন রঞ্জন (টেমপ্লেট:Lang-en) হচ্ছে, জটিল চলকের ফাংশনগুলিকে চিত্রিতকরণের একটি পদ্ধতি। ইংরেজি “ডোমেইন কালারিং” শব্দটা ১৯৯৮ সালের দিকে প্রথম ব্যবহার করেন ফ্রাঙ্ক ফেরিস [১] টেমপ্লেট:ওয়েব আর্কাইভ। কিন্তু ধারাবাহিক রঙ ব্যবহার করে ডোমেইন থেকে কো-ডোমেইনে বা ইমেজ প্লেনে ম্যাপ করার পদ্ধতিটা ১৯৯৯ সালে সর্বপ্রথম ব্যবহার করেন জর্জ আডো এবং পল গডফ্রে [২] টেমপ্লেট:ওয়েব আর্কাইভ গ্রাফিক্সে কালার গ্রিডের মাধ্যমে একে প্রকাশ করেন ডাহ্‌ আর্নল্ড ১৯৯৭ সালে [৩]।

উদ্দেশ্য

অপ্রতুল মাত্রা

একটি বাস্তব সংখ্যার ফাংশন $f:ℝ\to ℝ$ (যেমন $f(x)=x^2$) কে লেখচিত্রে দুইটি কার্তেসীয় স্থানাঙ্ক ব্যবহার করে একটা সমতলে অঙ্কন করা সম্ভব। একটি জটিল সংখ্যার ফাংশন $g:ℂ\to ℂ$ যেটার স্বাধীন চলক একটি এমনকি, তারও দুইটি জটিল বা কাল্পনিক মাত্রা থাকে। যেহেতু জটিল সমতল নিজেই দ্বিমাত্রিক সেহেতু একটা জটিল সংখ্যার ফাংশন তার দ্বিমাত্রিক আর্গুমেন্ট এবং দ্বিমাত্রিক মান নিয়ে আসলে একটা চতুর্মাত্রিক ব্যবস্থা। একারণে ত্রিমাত্রিক জগতে সেটাকে চিত্রিত করা মুশকিল। অবশ্য হোমোমর্ফিক ফাংশনসমূহ রিম্যান পৃষ্ঠতলের সাহায্যে প্রকাশ করা সম্ভব।

জটিল সংখ্যার দৃশ্যমান সাংকেতিকীকরণ

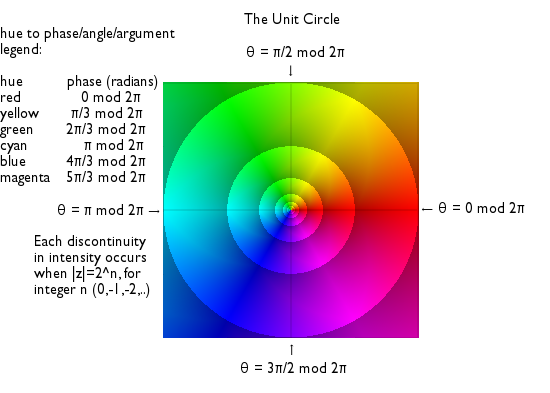
কোন একটা জটিল সংখ্যা $z=r{e}^{i\theta }$, এর ফেজ বা দশা(আরেক নাম আর্গুমেন্ট) $\theta$ কে হিউ বা রঙের পার্থক্য দ্বারা এবং মডুলাস বা মান $r=|z|$ কে তীব্রতা বা তীব্রতার পার্থক্য দ্বারা প্রকাশ করা হয়। দশা বোঝানোর জন্য রঙ গুলোকে ইচ্ছা মত নির্ধারণ করা যেতে পারে। তবে মাঝে মাঝে সেটা বর্ণচক্র (Color Wheel) অনুসারে হয়। কখনো কখনো দশা কে রঙের বদলে নির্দিষ্ট গ্রাডিয়েন্ট দ্বারা প্রকাশ করা হয়।

উদাহরণ

নিম্নে জটিল সংখ্যার সাইন ফাংশন $w=\sin (z)$ কে বাস্তব অক্ষ বরাবর$-2\pi$ থেকে $2\pi$ এবং কাল্পনিক অক্ষ বরাবর$-1.5$ থেকে $1.5$ পর্যন্ত নিয়ে উপরিউক্ত পদ্ধতিতে আঁকা হল।

তথ্যসূত্র

http://www.ima.umn.edu/~arnold/complex.html টেমপ্লেট:সূত্র তালিকা

বহিঃসংযোগ সমূহ

• Color Graphs of Complex Functions
• Visualizing complex-valued functions in the plane. টেমপ্লেট:ওয়েব আর্কাইভ
• Gallery of Complex Functions
• Complex Mapper by Alessandro Rosa
• John Davis software - S-Lang script for Domain Coloring