মজুমদার-ঘোষ মডেল

মজুমদার-ঘোষ মডেলটি একমাত্রিক কোয়ান্টাম হেইসেনবার্গের স্পিন মডেলের একটি সম্প্রসারণ, যেখানে একটি অতিরিক্ত মিথস্ক্রিয়া দ্বারা পরস্পর ঘূর্ণনযুক্ত দুটি ল্যাটিস যুক্ত হয় এবং দ্বিতীয় প্রতিবেশী জোড়টি প্রথমটির সাপেক্ষে অর্ধেক শক্তিশালী হয়। এটি J1 J2 মডেলের একটি বিশেষ ধারণা। ভারতীয় পদার্থবিজ্ঞানী চঞ্চল কুমার মজুমদার ও দীপন ঘোষের নামানুসারে এই মডেলের নামকরণ করা হয়।

মজুমদার-ঘোষ মডেলটি খুবই উল্লেখযোগ্য, কারণ এটির ভূমিস্তর (সর্বনিম্ন শক্তি কোয়ান্টাম স্তর) সঠিকভাবে পাওয়া যায় ও সহজ আকারে লিখিত হতে পারে। আরও জটিল ঘূর্ণন মডেল এবং পর্যায়গুলি বোঝার জন্য এটি একটি কার্যকর সূচনা করে।

সংজ্ঞা

মজুমদার-ঘোষ মডেলটি নিম্নলিখিত হ্যামিল্টনিয়ান (কোয়ান্টাম বলবিজ্ঞান) দ্বারা সংজ্ঞায়িত করা হয়েছে:

$\hat{H}=J\sum _{j=1}^N{\overrightarrow{S}}_j\cdot {\overrightarrow{S}}_{j+1}+\frac{J}{2}\sum _{j=1}^N{\overrightarrow{S}}_j\cdot {\overrightarrow{S}}_{j+2}$

যেখানে S ভেক্টরটি হল কোয়ান্টাম স্পিন অপারেটর এবং এর কোয়ান্টাম নম্বর S = ১/২ দ্বারা চিহ্নিত। সমবায়দের জন্য অন্যান্য সম্মেলনগুলি সাহিত্যে নেওয়া যেতে পারে, তবে সবচেয়ে গুরুত্বপূর্ণ বিষয় হল প্রথম প্রতিবেশী জোড় ও দ্বিতীয়-প্রতিবেশী জোড়ের অনুপাত ২:১।

সর্বনিম্ন শক্তিস্তর

মজুমদার-ঘোষ মডেল থেকে দুটি ন্যূনতম শক্তি স্তর পাওয়া যায়, যেখানে প্রতিবেশী ঘূর্ণন যুগ্ম একক কনফিগারেশন গঠন করে। প্রতিটি স্থল রাষ্ট্রের জন্য তরঙ্গাকৃতি এই একক জোড়াগুলির একটি পণ্য। এটি ব্যাখ্যা করে কেন একই শক্তির সাথে কমপক্ষে দুটি স্থল রাষ্ট্র থাকতে হবে, কারণ একটিকে অন্যতম স্থান থেকে কেবল একত্রিত করা, বা অনুবাদ করে, এক জ্যাকেট ফাঁক দ্বারা সিস্টেম থেকে নেওয়া যেতে পারে। প্রতিটি ভূমি স্তরের জন্য তরঙ্গাকৃতি এই একক জোড়াগুলি গঠন করে।

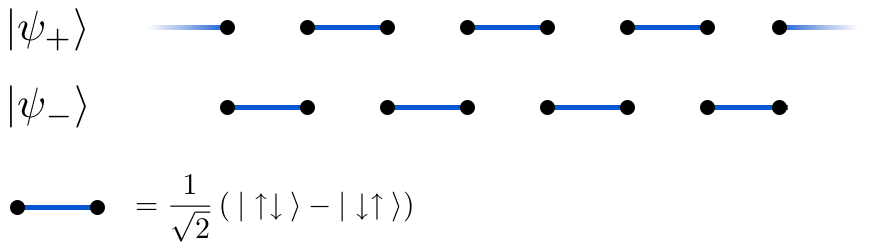
সরলীকরণ

মজুমদার-ঘোষ মডেলটি একটি ছোট মুষ্টিমেয় বাস্তবিক কোয়ান্টাম স্পিন মডেলগুলির মধ্যে একটি, যা সঠিকভাবে সমাধান করা যেতে পারে। তাছাড়া, এর নিম্নস্তরগুলি ভ্যালেন্স-বন্ড সলিড (ভিবিএস)-এর সাধারণ উদাহরণ। মজুমদার-ঘোষ মডেলটি অন্য একটি বিখ্যাত ঘূর্ণন মডেল, এএকেএলটি(AKLT) মডেলের সঙ্গে সম্পর্কিত। মজুমদার-ঘোষ মডেলটি লেব-শ্লুটজ-ম্যাটিস থিওরেম এরও একটি গুরুত্বপূর্ণ উদাহরণ, যা ব্যক্ত করে যে একটি অসীম, একমাত্রিক, অযুগ্ম পূর্ণসংখ্যা স্পিন পদ্ধতিতে তার সর্বনিম্ন শক্তিস্তর এবং উত্তেজিত শক্তিস্তরের মধ্যে কোনও শক্তিস্তর (বা ফাঁক) থাকতে পারে না অথবা একাধিক শক্তিস্তর রয়েছে। মজুমদার-ঘোষ মডেলের ক্ষেত্রে দুটি স্তরের (সর্বনিম্ন ও উত্তেজিত শক্তিস্তর) মধ্যে শক্তিস্তর রয়েছে, যা দ্বিতীয় বিষয়টির সঙ্গে সংগতিপূর্ণ।

আরো দেখুন

• হাইজেনবার্গের কোয়ান্টাম মডেল
• হাইজেনবার্গের ক্লাসিক্যাল মডেল
• J1 J2 মডেল
• t-J মডেল