প্রতিসরাঙ্ক

একটি প্লাস্টিক ব্লকে আলো প্রতিসরিত হচ্ছে

আলোকবিজ্ঞানে কোনো উপাদানের প্রতিসরাঙ্ক বা প্রতিসরণাঙ্ক বলতে ঐ উপাদানের মধ্য দিয়ে আলো কতটা দ্রুত অতিবাহিত হয় তার একটি মাত্রাহীন সংখ্যা। এটি সংজ্ঞায়িতঃ $n=\frac{c}{v}$,

যেখানে $c$ হলো শূন্য মাধ্যমে আলোর বেগ এবং $v$ হলো ঐ নির্দিষ্ট উপাদানে আলোর দশাবেগ। উদাহরণস্বরূপ পানির প্রতিসরাঙ্ক ৪/৩ বলতে বুঝায় শূন্য মাধ্যমে আলোর বেগ পানিতে আলোর বেগ অপেক্ষা ৪/৩ গুণ বেশি।

প্রতিসরাঙ্ক নির্দেশ করে কোনো উপাদানের মধ্য দিয়ে আলোকরশ্মি অতিবাহিত হওয়ার সময় কতটা প্রতিসরিত হয় বা আলোর পথ কতটা বেঁকে যায়। এটি স্নেলের প্রতিসরণের সূত্র দ্বারা ব্যাখ্যা করা হয়,

$n_1\sin {\theta }_1=n_2\sin {\theta }_2$

একটি আলোকরশ্মির প্রতিসরণ

যেখানে আলোকরশ্মি $n_1$ ও $n_2$ প্রতিসরাঙ্ক বিশিষ্ট দুটি ভিন্ন মাধ্যমের সংযোগস্থলে আপতিত হলে ${\theta }_1$ হলো আপতন কোণ এবং ${\theta }_2$ হলো প্রতিসরণ কোণ। প্রতিসরাঙ্ক আরও ধারণা দেয় দুটি ভিন্ন মাধ্যমের সংযোগস্থলে আলো কতটা প্রতিসরিত হয়, পূর্ণ অভ্যন্তরীণ প্রতিফলনে ক্রান্তি কোণ, ব্রূস্টার কোণ ইত্যাদি ব্যাপারে।

প্রতিসরাঙ্ককে এভাবেও কল্পনা করা যেতে পারে যে, কোনো একটি মাধ্যমে আলোর বেগ এবং তড়িৎ চৌম্বকীয় বিকিরণের তরঙ্গদৈর্ঘ্য এদের শূন্য মাধ্যমের মানের তুলনায় কতগুণ পরিবর্তিত হয়ঃ ঐ মাধ্যমে আলোর বেগ, $v=c/n$ এবং একইভাবে কোনো মাধ্যমে তড়িৎ চৌম্বকীয় বিকিরণের তরঙ্গদৈর্ঘ্য, $\lambda ={\lambda }_0/n$, যেখানে ${\lambda }_0$ হলো শূন্য মাধ্যমে আলোর তরঙ্গদৈর্ঘ্য। এটি হতে স্পষ্ট যে শূন্য মাধ্যমের প্রতিসরাঙ্ক $1$ এবং যেকোনো মাধ্যমে কম্পাঙ্ক প্রতিসরাঙ্কের উপর নির্ভরশীল নয়, কেননা কম্পাঙ্ক, $f=v/\lambda$। ফলস্বরূপ মানুষের চোখে প্রতিসরিত আলোকরশ্মি যা কম্পাঙ্কের উপর নির্ভরশীল হলেও মাধ্যমের প্রতিসরাঙ্কের উপর নির্ভরশীল নয়।

প্রতিসরাঙ্ক তরঙ্গদৈর্ঘ্যকে প্রভাবিত করলেও এটি কম্পাঙ্ক, আলোর বর্ণ এবং শক্তির উপর নির্ভর করে। তাই এসবের সম্মিলিত প্রভাবের ফলে সাদা আলো বিভিন্ন বর্ণে বিভক্ত হয়ে পড়ে যা আলোর বিচ্ছুরণ নামে পরিচিত। আলোর এই ধর্ম পরিলক্ষিত হয় প্রিজম এবং রংধনুতে।

আলোর প্রতিসরাঙ্কের ধারণা এক্স-রশ্মি হতে রেডিও তরঙ্গ তথা সম্পূর্ণ তড়িৎ চৌম্বকীয় বর্ণালি জুড়েই প্রযোজ্য। এছাড়াও এ ধারণা অন্যান্য তরঙ্গ সংশ্লিষ্ট ঘটনা, যেমনঃ শব্দ তরঙ্গের ক্ষেত্রেও প্রযোজ্য। এক্ষেত্রে আলোর বেগের পরিবর্তে শব্দের বেগ এবং শূন্য মাধ্যম ব্যতীত অন্য কোনো মাধ্যমকে বিবেচনায় নেয়া হয়।

সংজ্ঞা

প্রতিসরাঙ্ক সংজ্ঞায়িত শুন্য মাধ্যমে আলোর বেগ, $c=299792458m/s$ ও কোনো একটি মাধ্যমে আলোর দশাবেগের অনুপাত দ্বারা,

$n=\frac{c}{v}$

উপর্যুক্ত সংজ্ঞা কোনো কোনো ক্ষেত্রে অন্য কোনো সাপেক্ষ মাধ্যমে আলোর বেগের সাথে প্রভেদ করার জন্য একে বলা হয়ে থাকে পরম প্রতিসরাঙ্ক। ঐতিহাসিকভাবে প্রমাণিত তাপমাত্রা ও চাপে বাতাসকে সাধারণত সাপেক্ষ মাধ্যম হিসেবে ব্যবহার করা হয়।

ইতিহাস

থমাস ইয়াং সর্বপ্রথম প্রতিসরাঙ্ক নামটি ব্যবহার করেন

ধারণা করা হয় ১৮০৭ খ্রিষ্টাব্দে থমাস ইয়াং সর্বপ্রথম প্রতিসরাঙ্ক নামটি ব্যবহার করেন। সেই সময় তিনি প্রতিসরাঙ্কের মান প্রচলিত দুটি উপাদানের প্রতিসরাঙ্কের মানের অনুপাতের বদলে একটি সংখ্যা হিসেবে প্রকাশ করেন। অনুপাতের ক্ষেত্রে একই উপাদানের জন্য ভিন্ন ভিন্ন উপাদানের সাপেক্ষে অনুপাতসমূহ ভিন্ন হওয়ায় তা অসুবিধাজনক ছিল। আইজ্যাক নিউটন প্রতিসরাঙ্ককে বলেন, "proportion of the sines of incidence and refraction," এবং একে দুটি সংখ্যার অনুপাত হিসেবে উল্লেখ করেন, যেমনঃ "529 to 396" (অথবা প্রায় ৪/৩; পানির জন্য)। হক্সবি একে বলেন, "ratio of refraction," এবং একটি নির্দিষ্ট লবের সাপেক্ষে অনুপাত হিসেবে প্রকাশ করেন, যেমনঃ "10000 to 7451.9" (মূত্রের জন্য)। হাটন একে নির্দিষ্ট হরের সাপেক্ষে অনুপাত হিসেবে প্রকাশ করেন, যেমনঃ "1.3358 to 1"(পানি)।

১৮০৭ খ্রিষ্টাব্দে, ইয়াং প্রতিসরাঙ্কের জন্য কোনো প্রতীক ব্যবহার করেননি। পরবর্তীতে অন্যান্য বিজ্ঞানীগণ $n,m,\mu$ প্রভৃতি প্রতীক ব্যবহার করেন। ধীরে ধীরে $\mu$ প্রতীকটি প্রচলিত হয়ে উঠে।

আদর্শ মান

দৃশ্যমান আলোর জন্য বেশিরভাগ স্বচ্ছ মাধ্যমের প্রতিসরাঙ্ক ১ হতে ২ এর মধ্যে বিদ্যমান। সংযুক্ত ছকে কিছু পদার্থের প্রতিসরাঙ্ক দেয়া হলো। এক্ষেত্রে প্রতিসরাঙ্কের মানসমূহ সাধারনভাবে ব্যবহৃত ৫৮৯ ন্যানোমিটার তরঙ্গদৈর্ঘ্য বিশিষ্ট আলোকবর্ণালীর(হলুদ) সোডিয়ামের D-line জোড়ার জন্য পরিমাপকৃত। ছক হতে দেখা যায়, আদর্শ অবস্থায় গ্যাসের প্রতিসরাঙ্ক ১ এর কাছাকাছি। এর কারণ গ্যাসের নিম্ন ঘনত্ব। আবার বেশিরভাগ তরল ও কঠিন উপাদানের ক্ষেত্রে প্রতিসরাঙ্ক ১.৩ এর মধ্যে বিদ্যমান।

উপাদান	$n$
শুন্য মাধ্যম	১
$0^{\circ }$ এবং $1$ বায়ুমণ্ডলীয় চাপে গ্যাস
বায়ু	১.০০০২৯৩
হিলিয়াম	১.০০০০৩৬
হাইড্রোজেন	১.০০০১৩২
	১.০০০৪৫
$20^{\circ }$ তাপমাত্রায় তরল
পানি	১.৩৩৩
ইথানল	১.৩৬
জলপাই তেল	১.৪৭
কঠিন
বরফ	১.৩১
অস্ফটিক সিলিকা	১.৪৬
পলিমিথাইল মেথাক্রাইলেট	১.৪৯
জানালার কাঁচ	১.৫২
পলিকার্বনেট	১.৫৮
ফ্লিন্ট কাঁচ	১.৬২
নীলকান্তমণি	১.৭৭
ঘনক জিরকনিয়া	২.১৫
হীরক	২.৪২
ময়স্যানাইট	২.৬৫

একক অপেক্ষা কম প্রতিসরাঙ্ক

আপেক্ষিকতার সূত্র অনুযায়ী, কোনো তথ্য শুন্য মাধ্যমে আলোর বেগ অপেক্ষা দ্রুত হস্তান্তরিত করা সম্ভব নয়, কিন্তু তার মানে এই নয় যে প্রতিসরাঙ্ক ১ অপেক্ষা কম হতে পারবে না। প্রতিসরাঙ্ক পরিমাপ করে আলোর দশাবেগ যা তথ্য বহন করে না। দশাবেগ হলো তরঙ্গের শীর্ষ যে বেগে চলে যা শুন্য মাধ্যমে আলোর বেগ অপেক্ষা বেশি হতে পারে। এরূপ হতে পারে প্লাজমার শোষণ মাধ্যমে বা এক্স-রশ্মির জন্য অনুনাদ কম্পাঙ্কের কাছাকাছি অবস্থানে। এক্স-রশ্মি অঞ্চলে প্রতিসরাঙ্ক ১ অপেক্ষা কম, তবে ১ এর খুব কাছাকাছি (কিছু ব্যতিক্রম ব্যতীত)। উদাহরণস্বরূপ $30keV$ শক্তি বিশিষ্ট ফোটন কণার জন্য পানির প্রতিসরাঙ্ক $0.99999974=1-2.6\times 10^{-7}$।

প্লাজমার একক অপেক্ষা কম প্রতিসরাঙ্কের একটি উদাহরণ হলো পৃথিবীর আয়নস্ফিয়ার। চিত্র:Negative refraction through metamaterial prism.ogv

ঋণাত্মক প্রতিসরাঙ্ক

সাম্প্রতিক গবেষণা হতে দেখা যায় যে, ঋণাত্মক প্রতিসরাঙ্ক বিশিষ্ট উপাদানের অস্তিত্ব রয়েছে। এরূপ হতে পারে যদি কোনো উপাদানের আপেক্ষিক ভেদনযোগ্যতা ও ব্যাপ্তিযোগ্যতা উভয়ই একইসাথে ঋণাত্মক হয়। এটি পাওয়া যেতে পারে পর্যায়বৃত্তিকভাবে তৈরী মেটাউপাদানে।

প্রতিসরাঙ্কের আণুবীক্ষণিক ব্যাখ্যা

পারমাণবিক স্কেলে, কোনো উপাদানে একটি তড়িৎচুম্বকীয় তরঙ্গের দশাবেগ কমার কারণ তড়িৎক্ষেত্রে প্রতিটি পরমাণুর আধান(মূলত ইলেক্ট্রন) যে বিশৃঙ্খলা তৈরী করে তা ঐ মাধ্যমের তড়িৎগ্রাহিতার সমানুপাতিক। একইভাবে চৌম্বকক্ষেত্র চৌম্বকগ্রাহীতার সাথে সমানুপাতিক হারে বিশৃঙ্খলা তৈরী করে। তড়িৎচুম্বকীয় ক্ষেত্রসমূহ যখন তরঙ্গে স্পন্দিত হ্তে থাকে, ঐ উপাদানের ভিতর আধানসমূহ একটি নির্দিষ্ট কম্পাংকে সামনে পিছনে কম্পিত হতে থাকে। এভাবে আধানসমূহ একই কম্পাংক বিশিষ্ট নিজ তড়িৎচুম্বকীয় তরঙ্গ বিকিরণ করে, কিন্তু তা ঘটে কিছুটা দশা পার্থক্যে। আধানসমূহের উপর ক্রিয়াশীল বলের কারণে ধীরে ধীরে এরূপ দশা পার্থক্যের সৃষ্টি হয়। কোনো মাধ্যমে চলমান সকল আলোকরশ্মি হলো ঐ মাধ্যমে এরূপ সকল ম্যাক্রোস্কোপিক উপরিপাতনের সমষ্টিঃ মূল তরঙ্গ ও গতিশীল আধানের বিকিরণ তরঙ্গ। এই তরঙ্গ হলো সাধারণত একই কম্পাংক বিশিষ্ট, কিন্তু মূল তরঙ্গ অপেক্ষা ছোট তরঙ্গদৈর্ঘ্য বিশিষ্ট। কোনো উপাদানের আধানের এরকম কম্পনের ফলে সৃষ্ট বিকিরণ আপতিত তরঙ্গকে প্রভাবিত করে এবং এর বেগ পরিবর্তন করে। তবে কিছু পরিমাণ শক্তি অন্যান্য দিকে অথবা অন্য কোনো কম্পাংকে বিকিরিত হবে।(দেখুন বিচ্ছুরণ)

প্রাথমিক তরঙ্গ ও আধানের বিকিরিত তরঙ্গের আপেক্ষিক দশার উপর ভিত্তি করে বেশকিছু সম্ভাব্য ঘটনা ঘটতে পারেঃ

• যদি ইলেক্ট্রন $90^{\circ }$দশা পার্থক্যে আলো বিকিরণ করে, তবে তা মূল আলোকরশ্মির বেগ হ্রাস করে। এর ফলে প্রতিসরাঙ্ক হয় বাস্তব ও ১ অপেক্ষা বড়।
• যদি ইলেক্ট্রন $270^{\circ }$দশা পার্থক্যে আলো বিকিরণ করে, তবে তরঙ্গের বেগ মূলবেগ অপেক্ষা বৃদ্ধি পাবে। একে বলা হয় "ব্যতিক্রমী প্রতিসরণ", এবং এটি দেখা যায় শোষণ বর্ণালীর কাছাকাছি অবলোহিত বিকিরণ অঞলে, সাধারণ উপাদানের এক্স-রশ্মি এবং পৃথিবীর আয়নস্ফিয়ারে রেডিও তরঙ্গে। ভেদনযোগ্যতা একক অপেক্ষা কম হলে তথা আলোর দশাবেগ শুন্য মাধ্যমে আলোর বেগ অপেক্ষা বেশি হলে এরূপ ঘটনা ঘটে থাকে।
• যদি ইলেক্ট্রন $180^{\circ }$দশা পার্থক্যে আলো বিকিরণ করে, তবে তা মূল আলোকরশ্মির সাথে ধ্বংসাত্মক ব্যতিচার করবে এবং আপতিত আলোকরশ্মির তীব্রতা হ্রাস করবে। এরকম দেখা যায় যখন আলো অস্বচ্ছ মাধ্যমে শোষিত হয় এবং এর ফলে প্রতিসরাঙ্ক হয় কাল্পনিক।
• যদি ইলেক্ট্রন সমদশায় বিকিরিত হয় তবে আলোকরশ্মির বিবর্ধন হবে। এরূপ কদাচিৎ ঘটে থাকে, লেজাররশ্মির উত্তেজিত নিঃসরণের ফলে হয়। এর জন্যও প্রতিসরাঙ্ক কাল্পনিক হয়, তবে এর চিহ্ন হয় শোষণের বিপরীত।

বেশিরভাগ উপাদানের জন্য দৃশ্যমান আলোতে দশা পার্থক্য $90^{\circ }$হতে $180^{\circ }$এর মধ্যে বিদ্যমান থাকে যা প্রতিসরণ ও শোষণের সম্মিলন বলা যেতে পারে।

বিচ্ছুরণ

পানিতে বিভিন্ন বর্ণের আলোকরশ্মির প্রতিসরাঙ্কের কিছুটা পার্থক্য থাকার কারণে রংধনুতে ভিন্ন ভিন্ন অবস্থা দেখা যায়।

প্রিজমে আলোকরশ্মির বিচ্ছুরণের ফলে সাদা আলো বিভিন্ন রংএ বিভক্ত হয়।

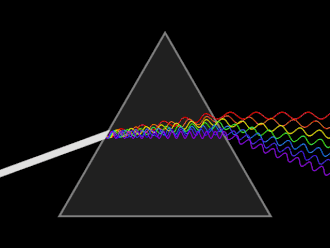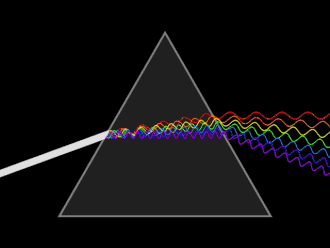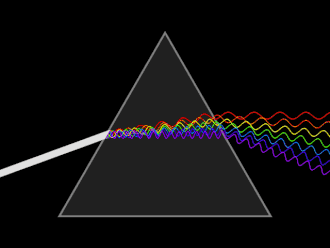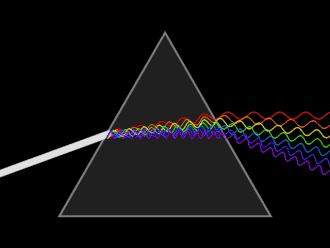
কোনো উপাদানের প্রতিসরাঙ্ক নির্ভর করে আলোকরশ্মির তরঙ্গদৈর্ঘ্য ও কম্পাংকের উপর। আলোর এ ধর্মকে বলা হয় বিচ্ছুরণ এবং এর কারণেই প্রিজম ও রংধনু সাদা আলোকে নিজ নিজ বর্ণালীগত উপাদানে বিভক্ত করে দেয়। প্রতিসরাঙ্কের তরঙ্গদৈর্ঘ্যের উপর নির্ভরশীলতার দরুণ এক উপাদান হতে অন্য উপাদানে আলো যাওয়ার পথে প্রতিসরণ কোণ পরিবর্তন হয়। বিচ্ছুরণের কারণেই লেন্সের ফোকাস দূরত্ব তরঙ্গদৈর্ঘ্যের উপর নির্ভরশীল।

দৃশ্যমান আলোর ক্ষেত্রে কোনো লেন্সে বিচ্ছুরণের পরিমাণকে আ্যবে সংখ্যা দ্বারা প্রকাশ করা হয়ঃ

$V=\frac{n_{yellow}-1}{n_{blue}-n_{red}}$

বিভিন্ন কাচের জন্য তরঙ্গদৈর্ঘ্যের সাথে প্রতিসরাঙ্কের পরিবর্তন। ছায়াকৃত অংশ নির্দেশ করে দৃশ্যমান আলো।

প্রতিসরাঙ্কের তরঙ্গদৈর্ঘ্যের উপর নির্ভরশীলতার আরও যথাযথ বর্ণনার জন্য ব্যবহার করা হয় সেলমিয়ার-এর সূত্র।

জটিল প্রতিসরাঙ্ক

আলো যখন কোনো একটি মাধ্যম অতিক্রম করে, সর্বদা আলোর কিছু অংশের ক্ষয় হবে। এই বিষয়টিকে বিবেচনায় আনা যায় জটিল প্রতিসরাঙ্ক সংজ্ঞায়িত করার মাধ্যমে,

$\underset{\_}{n}=n+i\kappa$

এখানে, সমীকরণটির বাস্তব অংশ, $n$ হলো প্রতিসরাঙ্ক, আর কাল্পনিক অংশ $\kappa$ কে বলা হয় বিলোপ সহগ। তবে $\kappa$ কে ভর ক্ষয় গুণাঙ্কও বলা হয়ে থাকে। এর দ্বারা প্রকাশ পায় তড়িৎচুম্বকীয় তরঙ্গ ঐ মাধ্যম অতিক্রমের বেলায় কি পরিমাণ ক্ষয়িত হয়।

$\kappa$ দ্বারা নির্দেশিত ক্ষয়কে $z$- অক্ষ বরাবর চলমান সমতলীয় তড়িৎচুম্বকীয় তরঙ্গের রাশিতে প্রতিসরাঙ্ক অন্তর্ভুক্ত করেও কল্পনা করা যেতে পারে। $\underset{\_}{k}=2\pi \underset{\_}{n}/{\lambda }_0$, এই সমীকরণে জটিল তরঙ্গ সংখ্যা $\underset{\_}{k}$ কে জটিল প্রতিসরাঙ্কের সাথে তুলনা করে তা সমতলীয় তড়িৎচুম্বকীয় তরঙ্গের রাশিতে পরিণত করে এটি করা যায়। এর ফলে সমতলীয় তড়িৎচুম্বকীয় তরঙ্গের সমীকরণটি দাঁড়ায়,

$\mathrm{E}(z,t)=Re[{\mathrm{E}}_0{e}^{i(2\pi ((n+ik)z/{\lambda }_0-\omega t)}=e^{-2\pi \kappa z/{\lambda }_0}Re[{\mathrm{E}}_0{e}^{i(kz-\omega t)}]$

এখানে দেখা যায় $\kappa$ সূচকীয় ক্ষয় দেয় যা বিয়ার-ল্যাম্বার্ট সূত্র থেকে অনুমিত। যেহেতু তীব্রতা তড়িতক্ষেত্রের বর্গের সমানুপাতিক, তাই এটি নির্ভর করে উপাদানের পুরুত্বের উপর $\exp (-4\pi \kappa /{\lambda }_0)$হিসেবে এবং ক্ষয় ধ্রুবক দাঁড়ায় $\alpha =4\pi \kappa /{\lambda }_0$। এটি আরও সম্পর্কায়িত করে ভেদন পুরুত্বের উপর, যেখানে ভেদন পুরুত্ব নির্দেশ করে ঐ পরিমাণ দূরত্ব যার পর তীব্রতা হ্রাস পেয়ে দাঁড়ায় $1/e,{\delta }_p=1/\alpha ={\lambda }_0/(4\pi \kappa )$।

$n$ ও $\kappa$ উভয়ই কম্পাংকের উপর নির্ভরশীল। বেশিরভাগ ক্ষেত্রে $\kappa >0$ (আলোর শোষণ) অথবা $\kappa =0$ (আলো ক্ষয় ব্যতীত চলমান)। বিশেষ ক্ষেত্রে $\kappa <0$ হতে পারে যা আলোর বিবর্ধন নির্দেশ করে।

অন্যান্য রাশির সাথে সম্পর্ক

আলোকীয় পথের দৈর্ঘ্য

আলোকীয় পথের দৈর্ঘ্য(ইংরেজিঃ Optical path length, OPL) হলো কোনো একটি ব্যবস্থায় আলোর অতিক্রান্ত জ্যামিতিক দৈর্ঘ্য এবং মাধ্যমের প্রতিসরাঙ্কের গুণফল,

$OPL=nd$

এটি আলোকবিজ্ঞানের একটি গুরুত্বপূর্ণ ধারণা, কেননা এটি আলোর দশা নির্ধারণ করে এবং আলোর চলার পথে ব্যতিচার ও অপবর্তন নিয়ন্ত্রণ করে। ফারম্যাটের নীতি অনুযায়ী, আলোকীয় পথ যে দৈর্ঘ্য অনুসরণ করে তা-ই হলো আলোকরশ্মি।

প্রতিসরণ

আলো যখন এক মাধ্যম হতে অপর মাধ্যমে স্থানান্তরিত হয়, তখন আলো দিক পরিবর্তন করে তথা প্রতিসরিত হয়। আলো যদি $n_1$ প্রতিসরাঙ্কের কোনো মাধ্যম হতে ${\theta }_1$ আপতন কোণে আপতিত হয়ে $n_2$ প্রতিসরাঙ্কের কোনো মাধ্যমে ${\theta }_2$ কোণে প্রতিসরিত হয়, তবে এই প্রতিসরণ কোণ পরিমাপ করা যায় স্নেলের প্রতিসরণের সূত্র দ্বারা,

$n_1\sin {\theta }_1=n_2\sin {\theta }_2$

আলো উচ্চতর প্রতিসরাঙ্কের কোনো মাধ্যমে প্রতিসরিত হলে প্রতিসরণ কোণ হবে ছোট এবং প্রতিসরিত আলোকরশ্মি অভিলম্বের দিকে সরে যাবে। আর আলো নিম্নতর প্রতিসরাঙ্কের কোনো মাধ্যমে প্রতিসরিত হলে প্রতিসরণ কোণ হবে বড় এবং প্রতিসরিত আলোকরশ্মি অভিলম্ব থেকে দূরে সরে যাবে।

পূর্ণ অভ্যন্তরীণ প্রতিফলন

যদি স্নেলের প্রতিসরণের সূত্র অনুযায়ী এমন কোনো প্রতিসরণ কোণ ${\theta }_2$ পাওয়া না যায়, অর্থাৎ

$\frac{n_1}{n_2}\sin {\theta }_1>1,$

হয়ে তবে আলো অপর মাধ্যমে স্থানান্তরিত না হয়ে আলোর পূর্ণ অভ্যন্তরীণ প্রতিফলন ঘটবে। এরকম ঘটনা ঘটে শুধুমাত্র যখন আলো উচ্চ আলোকীয় ঘনত্বসম্পন্ন কোনো মাধ্যম হতে নিম্ন আলোকীয় ঘনত্বসম্পন্ন কোনো মাধ্যমে প্রতিসরিত হয়। পূর্ণ অভ্যন্তরীণ প্রতিফলনের জন্য আপতন কোণ, ${\theta }_1$ অবশ্যই ক্রান্তি কোণ অপেক্ষা বড় হতে হবে, যেখানে ক্রান্তি কোণ

${\theta }_c=\arcsin \left(\frac{n_2}{n_1}\right)$

প্রতিবিম্বন

প্রতিসরিত আলো ছাড়াও কোনো মাধ্যমে আপতিত আলোর কিছু অংশ প্রতিফলিত হয়। এক্ষেত্রে, আপতন কোণ ও প্রতিফলন কোণ পরস্পর সমান হয় এবং এই প্রতিফলিত আলোর পরিমাণ নির্ধারিত হয় তলের প্রতিবিম্বনের উপর। প্রতিবিম্বন ফ্রেস্নেল এর সূত্র হতে প্রতিসরাঙ্ক এবং আপতন কোণ জানার মাধ্যমে নির্ণয় করা যায় যা লম্ব আপতনের জন্য দাঁড়ায়

$R_0={\left|\frac{n_1-n_2}{n_1+n_2}\right|}^2$

সাধারণ কাচের জন্য বাতাসে, $n_1=1$ এবং $n_2=1.5$; তাই ৪% এর মত আপতিত আলো প্রতিফলিত হয়। অন্যান্য আপতন কোণে প্রতিবিম্বন আলোর সমবর্তনের উপরও নির্ভর করে। ব্রূস্টার কোণ নামে পরিচিত একটি নির্দিষ্ট কোণে, সমবর্তিত আলো সম্পূর্ণভাবে স্থানান্তরিত হয়। এই কোণ দুটি মাধ্যমের প্রতিসরাঙ্ক হতে পরিমাপ করা যায়,

${\theta }_B=\arctan \left(\frac{n_2}{n_1}\right)$

লেন্স

কোনো একটি লেন্সের ফোকাস দূরত্ব নির্ধারণ করা হয় এর প্রতিসরাঙ্ক এবং তলের বক্রতার ব্যাসার্ধ $R_1$ ও $R_2$ দ্বারা। কোনো একটি সরু লেন্সের ক্ষমতা নির্ণয় করা হয় লেন্স প্রস্তুতকারকের সূত্র দ্বারা,

$\frac{1}{f}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})$

এখানে $f$ হলো লেন্সের ফোকাস দূরত্ব।

অণুবীক্ষণ যন্ত্র বিশ্লেষণ

আলোকীয় অণুবীক্ষণ যন্ত্রের বিশ্লেষণ ক্ষমতা পরিমাপ করা হয় প্রধানত এর অভিলক্ষ্য লেন্সের সংখ্যাসূচক অ্যাপারচার(NA) দ্বারা। এটি পরিমাপ করা হয় নমুনা ও লেন্সের মধ্যবর্তী স্থানের মাধ্যমের প্রতিসরাঙ্ক $n$ এবং নমুনা ও লেন্সের বীক্ষণ কোণ হতে,

$NA=n\sin \theta$

এ কারণে অধিক বিশ্লেষণ ক্ষমতা পাওয়ার জন্য তেল নিমজ্জন পদ্ধতি ব্যবহার করা হয়ে থাকে। এই পদ্ধতিতে অভিলক্ষ্য ও নমুনার মধ্যবর্তী স্থানে অধিক প্রতিসরাঙ্ক বিশিষ্ট তেল নিমজ্জন করা হয়।

আপেক্ষিক ভেদনযোগ্যতা ও ব্যাপ্তিযোগ্যতা

তড়িচ্চুম্বকীয় বিকিরণের প্রতিসরাঙ্ক

$n=\sqrt{{\epsilon }_r{\mu }_r}$,

যেখানে ${\epsilon }_r$ হলো উপাদানের আপেক্ষিক ভেদনযোগ্যতা ও ${\mu }_r$ হলো এর আপেক্ষিক ব্যাপ্তিযোগ্যতা। প্রতিসরাঙ্ক ব্যবহার করা হয় আলোকবিজ্ঞানে ফ্রেস্নেলের সমীকরণ ও স্নেলের সূত্রে; আর আপেক্ষিক ভেদনযোগ্যতা ও ব্যাপ্তিযোগ্যতা ব্যবহার করা হয় ম্যাক্সওয়েলের সমীকরণসমূহে এবং ইলেক্ট্রনিক্সে। বেশিরভাগ প্রকৃতিতে প্রাপ্ত উপাদান আলোক কম্পাংকে অচৌম্বকীয় তথা ${\mu }_r$ এর মান প্রায় ১ কাছাকাছি। অতএব, প্রতিসরাঙ্ক প্রায় $\sqrt{{\epsilon }_r}$। এই নির্দিষ্ট ক্ষেত্রে, জটিল আপেক্ষিক ভেদনযোগ্যতা ${\underset{\_}{\epsilon }}_r$ এর সাথে বাস্তব ও কাল্পনিক অংশ ${\epsilon }_r$ ও ${\tilde{\epsilon }}_r$; এবং জটিল প্রতিসরাঙ্ক $n$, যার বাস্তব ও কাল্পনিক অংশ $n$ এবং $\kappa$নিম্নোক্তভাবে সম্পর্কিত

${\underset{\_}{\epsilon }}_r={\epsilon }_r+i{\tilde{\epsilon }}_r={\underset{\_}{n}}^2=(n+i\kappa {)}^2,$

এবং এদের অংশকগুলো নিম্নরূপে সম্পর্কিতঃ

${\epsilon }_r=n^2-{\kappa }^2$,

${\tilde{\epsilon }}_r=2n\kappa$,

এবংঃ

$n=\sqrt{\frac{\left|{\underset{\_}{\epsilon }}_r\right|+{\epsilon }_r}{2}},$

$\kappa =\sqrt{\frac{\left|{\underset{\_}{\epsilon }}_r\right|-{\epsilon }_r}{2}},$

যেখানে, $\left|\underset{\_}{{\epsilon }_r}\right|=\sqrt{{\epsilon }_r^2+{\tilde{\epsilon }}^2}$ হলো জটিল মডুলাস।

তরঙ্গ প্রতিবন্ধকতা

কোনো সমতলীয় তড়িচ্চুম্বকীয় তরঙ্গের কোনো অপরিবাহী মাধ্যমে তরঙ্গ প্রতিবন্ধকতা,

$Z=\sqrt{\frac{\mu }{\epsilon }}=\sqrt{\frac{{\mu }_0{\mu }_r}{{\epsilon }_0{\epsilon }_r}}=\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}\sqrt{\frac{{\mu }_r}{{\epsilon }_r}}=Z_0\sqrt{\frac{{\mu }_r}{{\epsilon }_r}}=Z_0\frac{{\mu }_r}{n}$

যেখানে $Z_0$ হলো শূন্য মাধ্যমে তরঙ্গ প্রতিবন্ধকতা, $\mu$ ও $\epsilon$ হলো পরম ভেদনযোগ্যতা ও ব্যাপ্তিযোগ্যতা, ${\mu }_r$ ও ${\epsilon }_r$ হলো আপেক্ষিক ভেদনযোগ্যতা ও ব্যাপ্তিযোগ্যতা।

এমন কোনো অচৌম্বকীয় মাধ্যমে যেখানে ${\mu }_r=1$,

$Z=\frac{Z_0}{n}$,

$n=\frac{Z_0}{Z}$।

অতএব, কোনো অচৌম্বকীয় মাধ্যমে প্রতিসরাঙ্ক হলো শূন্য মাধ্যম এবং ঐ মাধ্যমে তরঙ্গ প্রতিবন্ধকতার অনুপাত।

তাই দুটি মাধ্যমের মধ্যকার প্রতিবিম্বন প্রতিসরাঙ্ক এবং তরঙ্গ প্রতিবন্ধকতা, উভয় দ্বারাই প্রকাশ করা যায়ঃ

$R_0={\left|\frac{n_1-n_2}{n_1+n_2}\right|}^2={\left|\frac{Z_2-Z_1}{Z_2+Z_1}\right|}^2.$

ঘনত্ব

সাধারণভাবে, কাচের প্রতিসরাঙ্ক এর ঘনত্ব বৃদ্ধির সাথে সাথে বৃদ্ধি পায়। কিন্তু সকল সিলিকেট এবং বোরোসিলিকেট কাচে প্রতিসরাঙ্ক এবং ঘনত্বের মধ্যে সরলরৈখিক সম্পর্ক বিদ্যমান নয়। অপেক্ষাকৃতভাবে উচ্চ প্রতিসরাঙ্ক এবং নিম্ন ঘনত্ব পাওয়া যায় হালকা ধাতুর অক্সাইড যেমন, $\mathrm{L}\mathrm{i}{\phantom{A}}_2\mathrm{O}$, $\mathrm{M}\mathrm{g}\mathrm{O}$ যুক্ত কাচ হতে। আর এর বিপরীত বৈশিষ্টের কাচে ব্যবহার করা হয় $\mathrm{P}\mathrm{b}\mathrm{O},\mathrm{B}\mathrm{a}\mathrm{O}$।

অনেক ধরনের তেল (যেমন, জল্পাই তেল) এবং ইথাইল অ্যালকোহল - এদের ক্ষেত্রে উচ্চ প্রতিসরাঙ্ক, কিন্তু পানি অপেক্ষা নিম্ন ঘনত্ব দেখা যায়।

বাতাসের ক্ষেত্রে, গ্যাসের রাসায়নিক গঠনের পরিবর্তন না হলে $n-1$, গ্যাসের ঘনত্বের সমানুপাতিক। অর্থাৎ এর থেকে আরও বলা যায় এটি আদর্শ গ্যাসের জন্য চাপের সমানুপাতিক এবং তাপমাত্রার ব্যস্তানুপাতিক।

গ্রুপ সূচক

মাঝে মাঝে, "গ্রুপ বেগ প্রতিসরাঙ্ক", যা সাধারণত গ্রুপ সূচক নামে পরিচিত, তা সংজ্ঞায়িতঃ

$n_g=\frac{c}{v_g}$

যেখানে $v_g$ হলো গ্রুপ বেগ। তবে এটি $n$ এর সাথে বিভ্রান্ত হওয়া যাবে না যা সবসময় দশাবেগের সাপেক্ষে সংজ্ঞায়িত। বিচ্ছুরণ কম হলে গ্রুপ বেগকে দশাবেগের সাথে সম্পর্কায়িত করা যায়,

$v_g=v-\lambda \frac{\mathrm{d}v}{\mathrm{d}\lambda },$

যেখানে $\lambda$ হলো ঐ মাধ্যমে তরঙ্গদৈর্ঘ্য। তাই এক্ষেত্রে গ্রুপ সূচককে লেখা যায়,

$n_g=\frac{n}{1+\frac{\lambda }{n}\frac{\mathrm{d}v}{\mathrm{d}\lambda }}$

যখন কোনো মাধ্যমের প্রতিসরাঙ্ক শূন্য মাধ্যমে তরঙ্গদৈর্ঘ্যের সাপেক্ষে জানা থাকে (ঐ মাধ্যমে তরঙ্গদৈর্ঘ্যের পরিবর্তে), সংশ্লিষ্ট গ্রুপ বেগ ও সূচক দাঁড়ায় (সকল বিচ্ছুরণের মানের জন্য)

$v_g=c(n-{\lambda }_0\frac{\mathrm{d}n}{\mathrm{d}{\lambda }_o}{)}^{-1},$

$n_g=n-{\lambda }_0\frac{\mathrm{d}n}{\mathrm{d}{\lambda }_0},$

যেখানে ${\lambda }_0$ হলো শূন্য মাধ্যমে তরঙ্গদৈর্ঘ্য।

অন্যান্য সম্পর্কসমূহ

ফিজাও এর পরীক্ষণ হতে দেখা যায়, যখন আলো কোনো চলমান মাধ্যমে স্থানান্তরিত হয়, তখন $v$ বেগে আলোর বেগের সাথে একই দিকে গতিশীল কোনো পর্যবেক্ষকের সাপেক্ষে এর বেগঃ

$V=\frac{c}{n}+\frac{v(1-\frac{1}{n^2})}{1+\frac{v}{cn}}\approx \frac{c}{n}+v(1-\frac{1}{n^2}).$

কোনো উপাদানের প্রতিসরাঙ্ক এর সমবর্তন হওয়ার ক্ষমতার সাথেও সম্পর্কিত।

অ-স্কেলার, অ-রৈখিক, অথবা অসমরূপী প্রতিসরণ

এ পর্যন্ত আমরা অনুমান করে নিয়েছি যে প্রতিসরাঙ্ক সরলরৈখিক সমীকরণ দ্বারা প্রকাশিত যাতে অন্তর্ভুক্ত স্থানিক ধ্রুবক, স্কেলার প্রতিসরাঙ্ক। এই অনুমানসমূহকে বিভিন্নভাবে ভেঙ্গে প্রকাশ করা যায় যা পরবর্তী অংশে আলোচ্য।

বাইরেফ্রিঞ্জেন্স

একটি কাগজের উপর স্থাপিত ক্যালসাইট স্ফটিকে কিছু অক্ষরের দ্বিগুণ প্রতিসরণ

কিছু উপাদানে প্রতিসরাঙ্ক নির্ভর করে সমবর্তন এবং আলোর চলার দিকের উপর। একে বলা হয় বাইরেফ্রিঞ্জেন্স অথবা আলোক অ্যানিসট্রোপি।

বাইরেফ্রিঞ্জেন্ট উপাদানকে আড়াআড়ি সমবর্তকের মাঝে রাখলে তার ফলে বিভিন্ন রংএর উদ্ভব ঘটতে পারে। এটিই ফটোইলাস্টিসিটির ভিত্তি।

একেবারে সাধারণ ক্ষেত্রে তথা একাক্ষিক বাইরেফ্রিঞ্জেন্সে, উপাদানের কেবল একটি বিশেষ দিক বিদ্যমান। এই অক্ষটি উপাদানের আলোক অক্ষ নামে পরিচিত। এই অক্ষের উপর লম্ব রৈখিক সমবর্তিত আলো যা স্বাভাবিক প্রতিসরাঙ্ক $n_0$ অনুভব করবে, আর এই অক্ষের সাথে সমান্তরালে থাকা আলো অনুভব করবে অস্বাভাবিক প্রতিসরাঙ্ক $n_e$। উপাদানের বাইরেফ্রিঞ্জেন্স হলো এই দুই প্রতিসরাঙ্কের পার্থক্য, $△n=n_e-n_o$। আলোক অক্ষের দিকে গতিশীল আলো বাইরেফ্রিঞ্জেন্স দ্বারা প্রভাবিত হবে না। অন্য চলার পথের জন্য আলো দুটি রৈখিকভাবে সমবর্তিত আলোকরশ্মিতে বিভক্ত হয়।

অনেক স্ফটিকই প্রকৃতিগতভাবে বাইরেফ্রিঞ্জেন্ট, কিন্তু আইসোট্রপিক উপাদানসমূহ যেমন, প্লাস্টিক এবং গ্লাসকে বহি:স্থ কোনো কাঙ্ক্ষিত বৈদ্যুতিক ক্ষেত্রে স্থাপনের মাধ্যমে বাইরেফ্রিঞ্জেন্ট বানানো যায়। এই প্রভাবকে বলা হয় ফটোইলাস্টিসিটি এবং তা ব্যবহার করে গঠনে কাঠিন্য/দৃঢ়তা বের করা যায়। বাইরেফ্রিঞ্জেন্ট উপাদানকে আড়াআড়ি সমবর্তকের মাঝে স্থাপন করা হয়। বাইরেফ্রিঞ্জেন্টের পরিবর্তন সমবর্তনকে পরিবর্তন করে এবং সেই সাথে দ্বিতীয় সমবর্তকে স্থানান্তরিত আলোর পরিমাণেরও পরিবর্তন করে।

ট্রাইরেফ্রিঞ্জেন্ট উপাদানের ক্ষেত্রে, ডাইইলেক্ট্রিক ধ্রুবক একটি ২য় ক্রমের টেন্সর (৩ বাই ৩ ম্যাট্রিক্স)।

অ-রৈখিকতা

শক্তিশালী বৈদ্যুতিক ক্ষেত্রের উচ্চ তীব্রতার ফলে কোনো মাধ্যমে আলো চলার পথে মাধ্যমের প্রতিসরাঙ্কের পরিবর্তন ঘটাতে পারে যা হতে অ-রৈখিক আলোকবিজ্ঞানের সৃষ্টি। যদি প্রতিসরাঙ্ক বৈদ্যুতিক ক্ষেত্রের সাথে দ্বিঘাত আকারে পরিবর্তিত হয় (তীব্রতার সাথে সরলরৈখিকভাবে), একে বলা হয় আলোকীয় কার প্রতিক্রিয়া এবং এর ফলে স্ব-ফোকাসিং এবং স্ব-দশা মডুলেশন হয়। যদি প্রতিসরাঙ্ক ক্ষেত্রের সাথে সরলরৈখিকভাবে পরিবর্তিত হয়, তবে তাকে বলা হয় পকেলের প্রতিক্রিয়া।

অসমরূপতা

একটি নতি-সূচক উপবৃত্তীয় লেন্স যার প্রতিসরাঙ্ক $n$ ও অরীয় দূরত্ব $x$। এই লেন্স প্রচলিত লেন্সের মতোই আলোকরশ্মি ফোকাসিত করে।

যদি কোনো মাধ্যমের প্রতিসরাঙ্ক ধ্রুব না হয়, বরং অবস্থানের সাথে সাথে ক্রমশ পরিবর্তিত হয়, তবে এর উপাদানকে বলা হয় নতি-সূচক অথবা GRIN মাধ্যম এবং এ সম্পর্কিত আলোকবিজ্ঞানকে নতিসূচক আলোকবিজ্ঞান বলা হয়। এরকম কোনো মাধ্যমে চলমান আলো বাঁকতে বা ফোকাসিত হতে পারে। আর এই প্রভাব কাজে লাগিয়ে লেন্স, কিছু অপটিকাল ফাইবার এবং অন্যান্য যন্ত্রপাতি তৈরি করা যায়। কোনো আলোকীয় সিস্টেমে GRIN উপাদানের অন্তর্ভুক্তি সিস্টেমের কর্মক্ষমতা রক্ষা করে সিস্টেমকে সহজ করতে পারে, উপাদান সংখ্যা কমাতে পারে প্রায় তিন ভাগের এক ভাগ পর্যন্ত। মানুষের চোখের স্ফটিকময় লেন্স হলো GRIN লেন্সের একটি উদাহরণ যার প্রতিসরাঙ্ক ভিতরের প্রকোষ্ঠে ১.৪০৬ হতে কম ঘনত্বের কর্টেক্সে প্রায় ১.৩৮৬ হতে পারে। কিছু প্রচলিত মরীচিকা ঘটে বাতাসে স্থানিকভাবে পরিবর্তিত প্রতিসরাঙ্কের জন্য।

প্রতিসরাঙ্ক পরিমাপ

সমসত্ত্ব মাধ্যম

অনেক রিফ্রাক্টোমিটারের মূলনীতি

তরল এবং কঠিন পদার্থ পরিমাপ করা যায় রিফ্রাকটোমিটার দ্বারা। এগুলো মূলত পরিমাপ করে প্রতিসরণ কোণ অথবা পূর্ণ অভ্যন্তরীণ প্রতিফলনের ক্রান্তি কোণ। ঊনবিংশ শতাব্দীর শেষদিকে আর্নেস্ট অ্যাবের বিকশিত ল্যাবরেটরি রিফ্রাকটোমিটার সর্বপ্রথম বাণিজ্যিকভাবে বিক্রয় শুরু হয়। এই একই নীতি বর্তমানে ব্যবহার করা হয়। এই যন্ত্রে যে তরলের প্রতিসরাঙ্ক পরিমাপ করা হবে তার একটি পাতলা স্তর দুটি প্রিজমের মাঝে স্থাপন করা হয়। $90^{\circ }$ পর্যন্ত আপতন কোণে আলো ঐ তরলে আপতিত করা হয় তথা তলের সমান্তরালে আলো আপতিত করা হয়। এক্ষেত্রে দ্বিতীয় প্রিজমের প্রতিসরাঙ্ক তরলের প্রতিসরাঙ্ক অপেক্ষা বেশি হওয়া প্রয়োজন যাতে তা পূর্ণ অভ্যন্তরীণ প্রতিফলনের ক্রান্তি কোণ অপেক্ষা ছোট হয়। এই কোণটি পরিমাপ করা যায় কোনো টেলিস্কোপ দিয়ে দেখার মাধ্যমে, অথবা আধুনিক ফটোডিটেক্টর লেন্সের ফোকাল তলে স্থাপনের মধ্যমে। তরলের প্রতিসরাঙ্ক $n$ পরিমাপ করা যায় সর্বোচ্চ ট্রান্সমিশন কোণ $\theta$ হতে, $n=n_G\sin \theta$; যেখানে $n_G$হলো প্রিজমের প্রতিসরাঙ্ক।

একটি হস্তচালিত রিফ্রাকটোমিটার যা দ্বারা ফলে বিদ্যমান চিনির পরিমাণ নির্ধারণ করা হয়

এ ধরনের যন্ত্র সাধারণত রাসায়নিক পরীক্ষাগারে নমুনা শনাক্তকরণ এবং মান নিয়ন্ত্রণে ব্যবহার করা হয়। হস্তচালিতগুলো ব্যবহার করা হয় কৃষিক্ষেত্রে এবং ইনলাইন প্রক্রিয়ার রিফ্রাকটোমিটার ব্যবহার করা হয় রাসায়নিক ও ঔষধ শিল্পে প্রক্রিয়া নিয়ন্ত্রণের কাজে।

মণিবিদ্যায় (gemology) ভিন্ন ধরনের রিফ্রাকটোমিটার ব্য বহার করা হয় রত্ন পাথরের প্রতিসরাঙ্ক পরিমাপ করার জন্য। এক্ষেত্রে রত্ন পাথরটি স্তাপন করা হয় উচ্চ প্রতিসরাঙ্কের প্রিজমে এবং তা নিচ হতে আলোকিত করা হয়। রত্ন এবং প্রিজমের মধ্যে আলোকীয় সংযোগ প্রাপ্তির জন্য একটি উচ্চ প্রতিসরাঙ্কের তরল ব্যবহার করা হয়। ক্ষুদ্র আপতন কোণের জন্য বেশিরভাগ আলো রত্ন-পাথরের মধ্য দিয়ে স্থানান্তরিত হলেও অধিক মানের আপতন কোণের জন্য প্রিজমে পূর্ণ অভ্যন্তরীণ প্রতিফলন ঘটে। এক্ষেত্রে ক্রান্তি কোণ সাধারণত পরিমাপ করা হয় টেলিস্কোপ দিয়ে দেখার মাধ্যমে।

প্রয়োগ

যেকোন আলোকীয় যন্ত্রের উপাদানের প্রতিসরাঙ্ক এর অত্যন্ত গুরুত্বপূর্ণ বৈশিষ্ট্য। এর দ্বারা নির্ণয় করা যায় লেন্সের ফোকাস ক্ষমতা, প্রিজমের বিচ্ছুরণ ক্ষমতা, লেন্স আবরণের প্রতিবিম্বন, এবং অপটিকাল ফাইবারের আলোক ধর্ম। যেহেতু প্রতিসরাঙ্ক কোনো উপাদানের অনন্য ভৌত বৈশিষ্ট্য, তাই এটি প্রায়ই ব্যবহার করা হয় কোনো নির্দিষ্ট উপাদান শনাক্তকরণে, এর বিশুদ্ধতা যাচাই, অথবা এর ঘনমাত্রা পরিমাপে। প্রতিসরাঙ্ক ব্যবহার করা হয় কঠিন, তরল ও গ্যাস পরিমাপণে। কোনো জলীয় দ্রবণে দ্রবের ঘনমাত্রা নির্ণয়ে এর ব্যাপক ব্যবহার দেখা যায়। এছাড়াও প্রতিসরাঙ্ক দ্বারা বিভিন্ন ধরনের রত্ন-পাথরের মধ্যে প্রভেদ করা হয়। রিফ্রাকটোমিটার দ্বারা কোনো উপাদানের প্রতিসরাঙ্ক পরিমাপ করা হয়। চিনির কোনো দ্রবণের জন্য প্রতিসরাঙ্ক হতে সে দ্রবণের চিনির পরিমাণ নির্ধারণ করা যায়।

আরও দেখুন

• ফার্মার নীতি
• কাচের বৈশিষ্ট্যের গণনা
• লেন্স
• এলিপসোমেট্রি
• প্রিজম
• ক্লসিয়াস-মসতি সম্পর্ক
• সম-প্রতিসরাঙ্ক উপাদান
• আলোর প্রতিসরণ
• আলোর প্রতিফলন
• আলোর বিচ্ছুরণ
• লেজার শ্লিরেন ডিফ্লেক্টমেট্রি
• পানি এবং বরফের আলোকীয় ধর্ম
• প্রিজম-কাপলিং ডিফ্লেক্টোমেট্রি
• লেজার
• আলোকীয় ঘনত্ব
• অপটিকাল ফাইবার