ফুরিয়ার ধারা

ফুরিয়ার ধারার প্রারম্ভিক এক, দুই, বা চার পদ দ্বারা বর্গ তরঙ্গ অপেক্ষকের (square wave function) সন্নিকটীকরণ (approximation)। অধিক পদ জুড়ে প্রাপ্ত গ্রাফ, বর্গ তরঙ্গের গ্রাফের সর্বাধিক নিকটবর্তী মনে হয়।

গণিতে ফুরিয়ার ধারা (Fourier series) এমন এক অসীম ধারা যা f পর্যায়ভুক্ত যেকোনো পর্যাবৃত্ত অপেক্ষককে (periodic function) f, 2f, 3f, ইত্যাদি পর্যায়ভুক্ত জ্যা ও সহ-জ্যা অপেক্ষকের যোগরূপে তৈরি করে। এর প্রয়োগ সর্বপ্রথম জোসেফ ফুরিয়ার (১৭৬৮ - ১৮৩০) ধাতুর প্লেটে তাপপ্রবাহ এবং তাপমাত্রার গণনার জন্য করেছিলেন। কিন্তু পরে এর ব্যবহার অনেক ক্ষেত্রে ঘটে এবং এটি বিশ্লেষণের একটি বৈপ্লবিক সামগ্রী প্রমাণিত হয়।

এর সহায়তায় অত্যধিক কঠিন অপেক্ষকও জ্যা ও সহ-জ্যা অপেক্ষকের যোগরূপে তৈরি করা হয় যা থেকে এ সম্পর্কিত গাণিতিক বিশ্লেষণ অত্যন্ত সরল হয়ে যায়।

ফুরিয়র ধারার প্রয়োগ

• তড়িৎ প্রকৌশলে - তড়িৎ তড়িৎক্ষেত্রে প্রবাহিত ধারা এবং বিভব ইত্যাদি গণনায়
• কম্পনের বিশ্লেষণে (যান্ত্রিক, শব্দ বা তড়িচ্চুম্বকীয় কম্পন)
• শব্দ, আলোর অধ্যয়ন এবং বিশ্লেষণে
• সঙ্কেত প্রক্রিয়াকরণে (signal processing)
• ছবি প্রক্রিয়াকরণে (image processing)

2π আবর্তনকালযুক্ত পর্যাবৃত্ত অপেক্ষকের জন্য ফুরিয়ার ধারা

ধরা হল, f(x), বাস্তব চল x এর একটি পর্যাবৃত্ত অপেক্ষক যার আবর্তন কাল হল 2π অর্থাৎ f(x+2π) = f(x) হলে,

$f(x)=\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}[a_n\cos (nx)+b_n\sin (nx)]$

এই ধারাকে ফুরিয়ার ধারা বলা হয়। $a_0,a_1,...$ ও $b_1,b_2,...$ কে ফুরিয়ার গুণাঙ্ক বলা হয়। এই গুণাঙ্ক বাস্তব সংখ্যা বা জটিল সংখ্যা হতে পারে।

$a_0=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)dx,$

$a_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\cos (nx)dx,$

$b_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\sin (nx)dx,$

ফুরিয়ার ধারার একটি সরল উদাহরণ

একটি করাতদাঁতী অপেক্ষকের (sawtooth function) গ্রাফ

করাতদাঁতী অপেক্ষকের জন্য ফুরিয়ার ধারার প্রথম পাঁচ পদের যোগ (এক পদ, দুই পদের যোগ, তিন পদের যোগ... ইত্যাদির) চলমান (animated) প্রদর্শন

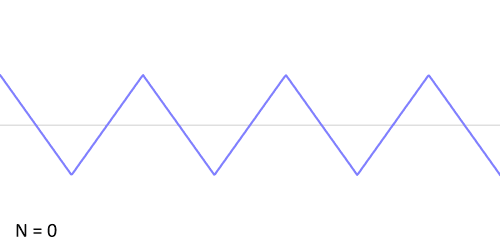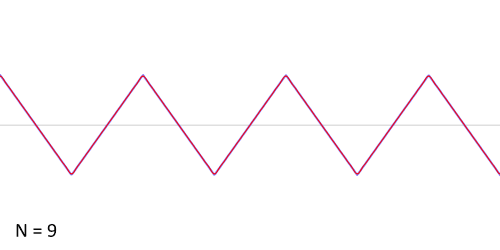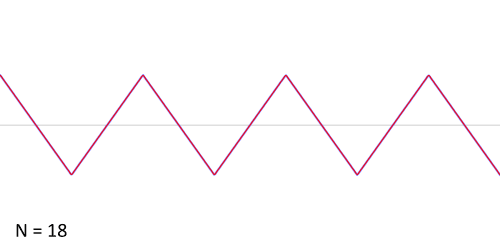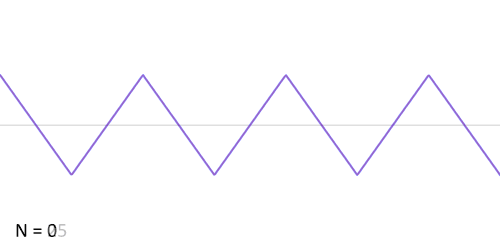
ধরা হল, প্রদত্ত অপেক্ষক করাতদাঁতী অপেক্ষক (sawtooth function) যাকে নিম্নলিখিত গাণিতিক পদ হিসাবে লেখা যায়:

$f(x)=x,\mathrm{f}\mathrm{o}\mathrm{r}-\pi <x<\pi ,$

$f(x+2\pi )=f(x),\mathrm{f}\mathrm{o}\mathrm{r}-\mathrm{\infty }<x<\mathrm{\infty }.$

এই অপেক্ষকের জন্য ফুরিয়ার গুণাঙ্ক এইধরনের:

$\begin{array}{cc}{a}_n& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}x\cos (nx)dx=0.\\ b_n& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}x\sin (nx)dx=2\frac{(-1{)}^{n+1}}{n}.\end{array}$

তাহলে

$\begin{array}{cc}f(x)& =\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}[a_n\cos \left(nx\right)+b_n\sin \left(nx\right)]\\ & =2\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}\sin (nx),\mathrm{f}\mathrm{o}\mathrm{r}-\mathrm{\infty }<x<\mathrm{\infty }.(*)\end{array}$

আরও দেখুন

• জোসেফ ফুরিয়ার
• ফুরিয়ার বিশ্লেষণ
• ফুরিয়ার রূপান্তর (Fourier transform)
• মূল পর্যায়

বহিঃসংযোগ

• Phasor Phactory Allows custom control of the harmonic amplitudes for arbitrary terms
• Java applet shows Fourier series expansion of an arbitrary function
• Example problems টেমপ্লেট:ওয়েব আর্কাইভ - Examples of computing Fourier Series
• Fourier series explanationটেমপ্লেট:অকার্যকর সংযোগ - A simple, non-mathematical approach
• Fourier Series Module by John H. Mathews
• Joseph Fourier - A site on Fourier's life which was used for the historical section of this article