চিত্র:VFPt dipoles magnetic.svg

এই ফাইলটি উইকিমিডিয়া কমন্স থেকে আগত এবং অন্যান্য প্রকল্পে ব্যবহৃত হতে পারে। সেখানে থাকা ফাইলটির বিবরণ পাতার বিবরণ নিচে দেখানো হলো।
সারাংশ
| বিবরণVFPt dipoles magnetic.svg |
English: Computed drawings of four different types of magnetic dipoles. Upper left: An ideal point-like dipole. The field shape is scale invariant and approximates the field of any magnetized volume with nonzero dipole moment at large distance. |
| তারিখ | |
| উৎস | নিজের কাজ |
| লেখক | Geek3 |
| অন্যান্য সংস্করণ | VFPt dipoles electric.svg |
| SVG genesis InfoField | switch elements: all translations are stored in the same file. |
| উৎস কোড InfoField | Python code# paste this code at the end of VectorFieldPlot 2.5
R = 0.6
h = 0.6
rsym = 21
doc = FieldplotDocument('VFPt_dipoles_magnetic1', commons=True,
width=360, height=360)
field = Field([ ['dipole', {'x':0, 'y':0, 'px':0., 'py':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return hypot(*xy) > 1e-4 and (fabs(xy[1]) < 1e-3 or fabs(xy[1]) > .3)
nlines = 19
startpoints = Startpath(field, lambda t: 0.25*sc.array([sin(t), cos(t)]),
t0=-pi/2, t1=pi/2).npoints(nlines)
for p0 in startpoints:
line = FieldLine(field, p0, directions='both')
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw dipole symbol
rg_grad = etree.SubElement(doc._get_defs(), 'linearGradient')
rg_grad.set('id', 'grad_rg')
for attr, val in [ ['x1', '0'], ['x2', '0'], ['y1', '0'], ['y2', '1'] ]:
rg_grad.set(attr, val)
for col, of in [ ['#00cc00', '0'], ['#887744', '0.5'], ['#ff0000', '1'] ]:
stop = etree.SubElement(rg_grad, 'stop')
stop.set('stop-color', col)
stop.set('offset', of)
stop.set('stop-opacity', '1')
symb = doc.draw_object('g', {'id':'dipole_symbol',
'transform':'scale({0},{0})'.format(1./doc.unit)})
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#grad_rg)', 'stroke':'none'}, group=symb)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'},
group=symb)
doc.draw_object('path', {'fill':'#000000', 'stroke':'none',
'd':'M 3,-12 V 0 H 12 L 0,15 L -12,0 H -3 V -12 H 3 Z'}, group=symb)
doc.write()
doc = FieldplotDocument('VFPt_dipoles_magnetic2', commons=True,
width=360, height=360)
field = Field([ ['monopole', {'x':0, 'y':h, 'Q':1}],
['monopole', {'x':0, 'y':-h, 'Q':-1}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return fabs(xy[0]) < 1.4
nlines = 18
stp = Startpath(field, lambda t: R*sc.array([.2*sin(t), 1+.2*cos(t)]),
t0=-pi, t1=pi)
startpoints = [stp.startpos(s) for s in sc.arange(nlines)/float(nlines)]
startpoints.append(startpoints[nlines//2].dot([ [1,0],[0,-1] ]))
for p0 in startpoints:
line = FieldLine(field, p0, directions='both', maxr=100)
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw pole symbols
symb_N = doc.draw_object('g', {'id':'north_symbol',
'transform':'translate(0,{0}) scale({1},{1})'.format(h, 1./doc.unit)})
symb_S = doc.draw_object('g', {'id':'south_symbol',
'transform':'translate(0,{0}) scale({1},{1})'.format(-h, 1./doc.unit)})
for i, g in enumerate([symb_N, symb_S]):
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym, 'stroke':'none',
'fill':['#ff0000', '#00cc00'][i]}, group=g)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'}, group=g)
text = etree.SubElement(g, 'text')
for attr, val in [ ['text-anchor', 'middle'], ['x', 0], ['y', 11],
['fill', '#000000'], ['stroke', 'none'], ['font-size', '32px'],
['font-family', 'Bitstream Vera Sans'],
['transform', 'scale(1, -1)'] ]:
text.set(attr, str(val))
text.text = ['N', 'S'][i]
doc.write()
doc = FieldplotDocument('VFPt_dipoles_magnetic3', commons=True,
width=360, height=360)
field = Field([ ['ringcurrent', {'x':0, 'y':0, 'R':R, 'phi':pi/2, 'I':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return hypot(*xy) > R and fabs(fabs(xy[0]) - 1.4) > 0.2
nlines = 13
startpoints = Startpath(field, lambda t: sc.array([R*t, 0.]),
t0=-0.8, t1=0.8).npoints(nlines)
for p0 in startpoints:
line = FieldLine(field, p0, directions='both')
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw current symbols
symb_out = doc.draw_object('g', {'id':'out_symbol',
'transform':'translate({0},0) scale({1},{1})'.format(-R, 1./doc.unit)})
symb_in = doc.draw_object('g', {'id':'in_symbol',
'transform':'translate({0},0) scale({1},{1})'.format(R, 1./doc.unit)})
for i, g in enumerate([symb_out, symb_in]):
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym, 'stroke':'none',
'fill':'#999999'}, group=g)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'}, group=g)
if i == 0: # dot
c_symb = etree.SubElement(g, 'circle')
c_symb.set('cx', '0')
c_symb.set('cy', '0')
c_symb.set('r', '6')
else: # cross
c_symb = etree.SubElement(g, 'path')
c_symb.set('d', 'M {1},{4} L {0},{5} L {2},{3} L {0},{1} \
L {1},{0} {3},{2} L {5},{0} L {4},{1} L {6},{3} L {4},{5} L {5},{4} \
L {3},{6} L {1},{4} Z'.format(12.24, 8, 4.24, 0, -12.24, -8, -4.24))
c_symb.set('style', 'fill:#000000; stroke:none')
doc.write()
doc = FieldplotDocument('VFPt_dipoles_magnetic4', commons=True,
width=360, height=360)
field = Field([ ['coil', {'x':0, 'y':0, 'phi':pi/2, 'R':R, 'Lhalf':h, 'I':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return sc.hypot(xy[0], xy[1]) > R
nlines = 13
for iline in range(nlines):
p0 = sc.array([R * (-1. + 2. * (iline + 0.5) / nlines), 0.])
line = FieldLine(field, p0, directions='both', maxr=100)
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw solenoid
sheet_out = doc.draw_object('g', {
'transform':'translate({0},0)'.format(-R)})
sheet_in = doc.draw_object('g', {
'transform':'translate({0},0)'.format(R)})
for i, g in enumerate([sheet_out, sheet_in]):
doc.draw_object('rect', {'stroke-width':0.03, 'stroke-linejoin':'round',
'x':-0.045, 'y':-h, 'width':0.09, 'height':2*h,
'stroke':'#000000', 'fill':'#bbbbbb'}, group=g)
nsym = 12
for isym in range(nsym):
y = (h - 0.015) * (2 * (isym + 0.5) / nsym - 1)
if i == 0:
doc.draw_object('circle', {'cx':'0', 'cy':y, 'r':0.02,
'fill':'#000000', 'stroke':'none'}, group=g)
else:
doc.draw_object('path', {'d':'M -2,-2 L 2,2 M -2,2 L 2,-2',
'fill':'none', 'stroke':'#000000',
'transform':'translate(0, {0}) scale(0.012)'.format(y),
'stroke-width':'1', 'stroke-linecap':'butt'}, group=g)
doc.write()
|
লাইসেন্স প্রদান
- আপনি স্বাধীনভাবে:
- বণ্টন করতে পারেন – এ কাজটি অনুলিপি, বিতরণ এবং প্রেরণ করতে পারেন
- পুনঃমিশ্রণ করতে পারেন – কাজটি অভিযোজন করতে পারেন
- নিম্নের শর্তাবলীর ভিত্তিতে:
- স্বীকৃতিপ্রদান – আপনাকে অবশ্যই যথাযথ স্বীকৃতি প্রদান করতে হবে, লাইসেন্সের একটি লিঙ্ক সরবরাহ করতে হবে এবং কোনো পরিবর্তন হয়েছে কিনা তা নির্দেশ করতে হবে। আপনি যেকোনো যুক্তিসঙ্গত পদ্ধতিতে এটি করতে পারেন। কিন্তু এমন ভাবে নয়, যাতে প্রকাশ পায় যে লাইসেন্সধারী আপনাকে বা আপনার এই ব্যবহারের জন্য অনুমোদন দিয়েছে।
- একইভাবে বণ্টন – আপনি যদি কাজটি পুনঃমিশ্রণ, রুপান্তর, বা এর ওপর ভিত্তি করে নতুন সৃষ্টিকর্ম তৈরি করেন, তবে আপনাকে অবশ্যই আপনার অবদান একই লাইসেন্স বা একই রকমের লাইসেন্সের আওতায় বিতরণ করতে হবে।
ক্যাপশন
এই ফাইলে চিত্রিত আইটেমগুলি
যা চিত্রিত করে
কিছু মানের উইকিউপাত্ত আইটেম নেই
১১ জানুয়ারি 2020
image/svg+xml
ফাইলের ইতিহাস
যেকোনো তারিখ/সময়ে ক্লিক করে দেখুন ফাইলটি তখন কী অবস্থায় ছিল।
| তারিখ/সময় | সংক্ষেপচিত্র | মাত্রা | ব্যবহারকারী | মন্তব্য | |
|---|---|---|---|---|---|
| বর্তমান | ১৭:২৫, ১১ জানুয়ারি ২০২০ | 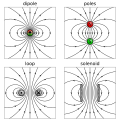 | ৮৪০ × ৮৪০ (১০৩ কিলোবাইট) | wikimediacommons>Geek3 | User created page with UploadWizard |
ফাইলের ব্যবহার
নিম্নলিখিত পাতাটি এই ফাইল ব্যবহার করে: