স্পর্শকীয় বৃত্তের ক্ষেত্রে কক্সেটারের লোক্সোড্রোমিক অনুক্রম
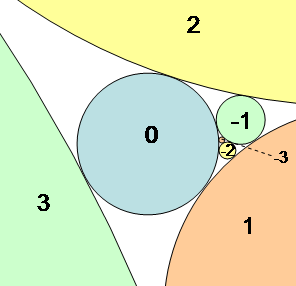
জ্যামিতিতে স্পর্শকীয় বৃত্তের ক্ষেত্রে কক্সেটারের লোক্সোড্রোমিক অনুক্রম হলো একাধিক বৃত্তের এমন এক অসীম অনুক্রম, যেখানে এই বৃত্তগুলো এমনভাবে সজ্জিত থাকে, যেন অনুক্রমটির ধারাবাহিক যেকোনো চারটি বৃত্ত জোড়ার জোড়ায় পরস্পরের স্পর্শক। এর মানে হলো, অনুক্রমটির প্রতিটি বৃত্ত তার পূর্ববর্তী তিনটি বৃত্তের স্পর্শক, উপরন্তু এই বৃত্তটি তার পরবর্তী বা অনুসরণকারী অন্য তিনটি বৃত্তেরও স্পর্শক।
ধর্ম
অনুক্রমটি যেসব বৃত্ত নিয়ে গঠিত সেই সব বৃত্তের ব্যাসার্ধসমূহ একটি গুণোত্তর প্রগমন গঠন করে, যেখানে সাধারণ অনুপাত হবে: এখানে হলো সোনালি অনুপাত। অনুপাত এবং এর ব্যাস্তানুপাত এই সমীকরণটি সিদ্ধ করে:
আর একারণেই, অনুক্রমটির ধারাবাহিক যেকোনো চারটি বৃত্ত দেকার্তের উপপাদ্যের শর্তের সাথে মিলে যায়।টেমপ্লেট:R
অনুক্রমে বিদ্যমান বৃত্তগুলো যে কেন্দ্রগুলো গঠন করে সেই কেন্দ্রগুলো একটি লগভিত্তিক স্পাইরালের ওপর অবস্থান করে। স্পাইরালটির কেন্দ্রের সাপেক্ষে বিবেচনা করা হলে, ধারাবাহিক বৃত্তগুলোর দুটি কেন্দ্রের মধ্যে অন্তর্ভুক্ত কোণটি হবে:টেমপ্লেট:R এবং কেন্দ্রগুলোর দুটো ত্রয়ীর মধ্যবর্তী কোণটি হবে: এই কোণটি কেপলার ত্রিভুজের একটি কোণের অনুরূপ। কেপলার ত্রিভুজ হলো এমন একটি সমকোণী ত্রিভুজ, যার গঠন আবার সোনালি অনুপাতের বর্গমূলের সাথে সম্পর্কযুক্ত।টেমপ্লেট:R
ইতিহাস এবং সংশ্লিষ্ট জ্যামিতিক কাঠামো
এই জ্যামিতিক কাঠামোটির নামকরণ করা হয়েছে জ্যামিতি শাস্ত্রবিদ (জিওমিটার) এইচ এস এম কক্সেটারের নামানুসারে, যিনি উচ্চতর মাত্রার গোলক এবং অধিগোলকের অনুক্রমের মধ্যে দ্বিমাত্রিক বিষয়বস্তুর সাধারণিকরণ করেছেন।টেমপ্লেট:R একে ডয়েল স্পাইরালের একটি অধঃপতিত বিশেষ ক্ষেত্র বা ঘটনারূপে ব্যাখ্যা করা যেতে পারে।টেমপ্লেট:R