তরঙ্গ দৈর্ঘ্য

একটি সাইন তরঙ্গ এবং λ এর তরঙ্গদৈর্ঘ্য একই।দশা (ফেজ) দিয়ে যেকোনো দুটি বিন্দুর মধ্যে পরিমাপ করা যায়

পদার্থবিজ্ঞানে তরঙ্গ সঞ্চালনকারী কোনো কম্পনশীল কণার একটি পূর্ণ কম্পন সম্পন্ন হতে যে সময় লাগে সেই সময়ে তরঙ্গ যে দূরত্ব অতিক্রম করে তাকে তরঙ্গদৈর্ঘ্য বলে এটি তরঙ্গের একই ফেজ এর পরপর সংশ্লিষ্ট বিন্দুর মধ্যে দূরত্ব। যেমন দুটি সংলগ্ন ক্রেস্ট, ট্রফ বা শূন্য ক্রসিং উভয়ই ট্রাভেলিং তরঙ্গের একটি বৈশিষ্ট্য এবং সেইসাথে অন্যান্য স্থানিক তরঙ্গের একটি নিদর্শন। তরঙ্গদৈর্ঘ্যের বিপরীত দিককে স্থানিক কম্পাঙ্ক বলে। তরঙ্গদৈর্ঘ্য সাধারণত গ্রিক অক্ষর ল্যাম্বডা (λ) দ্বারা চিহ্নিত হয়। তরঙ্গদৈর্ঘ্য শব্দটি কখনও কখনও মড্যুলেটেড তরঙ্গ এবং বিভিন্ন সাইনোসয়েডের হস্তক্ষেপ দ্বারা গঠিত মডুলেটেড তরঙ্গ বা তরঙ্গের সাইনোসয়েডাল খামেও প্রয়োগ করা হয়। উচ্চতর কম্পাঙ্কবিশিষ্ট তরঙ্গগুলির ছোট তরঙ্গদৈর্ঘ্য থাকে এবং নিম্ন কম্পাঙ্কবিশিষ্ট তরঙ্গগুলির দীর্ঘতর তরঙ্গদৈর্ঘ্য থাকে।

যে মাধ্যম দিয়ে তরঙ্গ চলাচল করে, সেই মাধ্যমের উপর তরঙ্গদৈর্ঘ্য নির্ভর করে। (উদাহরণস্বরূপ, ভ্যাকুয়াম, বায়ু বা জল)। তরঙ্গের উদাহরণ হল শব্দ তরঙ্গ, আলোকতরঙ্গ, জলতরঙ্গ এবং পর্যায়ক্রমিক বৈদ্যুতিক তরঙ্গ(যা একটি কন্ডাক্টর)। একটি শব্দ তরঙ্গ বায়ুর একটি পরিবর্তনের ফলে চাপ, আলো এবং অন্যান্য ইলেক্ট্রোম্যাগনেটিক রেডিয়েশন এবং চৌম্বক ক্ষেত্র পরিবর্তিত হয়। জলের তরঙ্গ হল জলের পৃষ্ঠের উচ্চতার তারতম্য। একটি স্ফটিক জালির কম্পন এ, পারমাণবিক অবস্থান পরিবর্তিত হয়।

তরঙ্গদৈর্ঘ্য বা কম্পাঙ্কের পরিসরকে বর্ণালী বলা হয়।বর্ণালী নামের উৎপত্তি দৃশ্যমান আলোর বর্ণালী থেকে। এখন সমগ্র ইলেক্ট্রোম্যাগনেটিক স্পেকট্রাম প্রয়োগ এর পাশাপাশি একটি শব্দ বর্ণালী বা কম্পন বর্ণালী প্রয়োগ করা যেতে পারে।

সাইন তরঙ্গ

রৈখিক মাধ্যমে, সাইন তরঙ্গের উপাদানগুলি স্বাধীন প্রচারের পরিপ্রেক্ষিতে যে কোনও তরঙ্গ প্যাটার্ন বর্ণনা করতে পারে। একটি সাইন তরঙ্গরূপের তরঙ্গদৈর্ঘ্য v ধ্রুব গতিতে চলাচল করে।

$\lambda =\frac{v}{f},$

এখানে v কে তরঙ্গের পর্যায় গতি (ফেজ বেগ) বলা হয় এবং f হল তরঙ্গের কম্পাঙ্ক। একটি বিচ্ছুরণ মাধ্যম-এ, ফেজ গতি নিজেই তরঙ্গের কম্পাঙ্কের উপর নির্ভর করে।

ইলেক্ট্রোম্যাগনেটিক রেডিয়েশন—যেমন আলোর ক্ষেত্রে—মুক্ত স্থান। ফেজের গতি হল আলোর বেগ- যা প্রায় ৩×১0^৮m/s। ইলেক্ট্রোম্যাগনেটিক (রেডিও) তরঙ্গের তরঙ্গদৈর্ঘ্য প্রায়: ৩×১০^৮m/s।দৃশ্যমান আলোর তরঙ্গদৈর্ঘ্য লাল থেকে মোটামুটি ৭০০ ন্যানোমিটার গভীর)।

বাতাসে শব্দ তরঙ্গ এর জন্য, শব্দের গতি হল ৩৪৩ m/s (রুমের তাপমাত্রা এবং বায়ুমণ্ডলীয় চাপ)। মানুষের কানে শ্রবণযোগ্য শব্দ ফ্রিকোয়েন্সিগুলির তরঙ্গদৈর্ঘ্য (২০ Hz–২০ kHz) এইভাবে যথাক্রমে প্রায় ১৭ মি এবং ১৭ মিমি এর মধ্যে, কিছুটা উচ্চতর কম্পাঙ্কগুলো বাদুড়ের দ্বারা ব্যবহৃত হয় যাতে তারা ১৭ মিমি থেকে ছোট লক্ষ্যগুলি সমাধান করতে পারে। শ্রবণযোগ্য শব্দের তরঙ্গদৈর্ঘ্য দৃশ্যমান আলোর চেয়ে অনেক বেশি।

একটি বাক্সে সাইন একটি স্থায়ী তরঙ্গ, যা শেষ বিন্দুগুলিকে নোড হিসাবে সীমাবদ্ধ করে এবং যা বাক্সে অর্ধেক তরঙ্গদৈর্ঘ্যের একটি পূর্ণসংখ্যায় ফিটিং করে।

একটি স্থায়ী তরঙ্গ (কালো) বিপরীত দিকে চলাচলকারী দুটি প্রচারকারী তরঙ্গের সমষ্টি হিসাবে চিত্রিত (লাল এবং নীল)

স্থির তরঙ্গ

একটি স্থির তরঙ্গ হলো একটি আন্দোলিত গতি, যা এক জায়গায় স্থির থাকে। একটি সাইনোসয়েডাল স্থায়ী তরঙ্গের মধ্যে একটি গতিহীন স্থির বিন্দু রয়েছে, যাকে নোড বলা হয় এবং তরঙ্গদৈর্ঘ্য নোডের মধ্যের দূরত্বের দ্বিগুণ।

উপরের চিত্রটিতে, একটি বাক্সে তিনটি স্থির তরঙ্গ দেখা যায়। বাক্সের দেয়াল, কোন তরঙ্গদৈর্ঘ্য অনুমোদিত তা নির্ধারণ করে। বাক্সের দেয়ালে নোড থাকা সত্ত্বেও তরঙ্গের প্রয়োজন বলে মনে করা হয় (সীমান্ত শর্তের একটি উদাহরণ)। উদাহরণস্বরূপ, একটি ইলেক্ট্রোম্যাগনেটিক তরঙ্গের জন্য যদি বাক্সে আদর্শ ধাতব দেয়াল থাকে, তাহলে দেয়ালের নোডগুলির অবস্থার পরিবর্তন হয়। কারণ ধাতব দেয়াল একটি স্পর্শক বৈদ্যুতিক ক্ষেত্রকে সমর্থন করতে পারে না, তরঙ্গটিকে দেয়ালে শূন্য প্রশস্ততায় থাকতে বাধ্য করে।

স্থির তরঙ্গকে বেগের পশ্চাৎ দিক নির্দেশিত দুটি গতিশীল সাইন তরঙ্গের সমষ্টি হিসাবে দেখা যায়। ফলস্বরূপ, তরঙ্গদৈর্ঘ্য, সময়কাল এবং তরঙ্গ বেগ একটি গতিশীল তরঙ্গের সাথে সম্পর্কিত। উদাহরণস্বরূপ, আলোর গতি একটি আদর্শ ভ্যাকুয়াম ধারণকারী ধাতব বাক্সে স্থির থাকা তরঙ্গের থেকে নির্ধারণ করা যায়।

গাণিতিক উপস্থাপনা

গতিশীল সাইন তরঙ্গগুলি প্রায়শই গাণিতিকভাবে তাদের বেগ v (x দিকে), কম্পাঙ্ক f এবং তরঙ্গদৈর্ঘ্য λ হিসাবে উপস্থাপন করা হয়:

$y(x,t)=A\cos \left(2\pi (\frac{x}{\lambda }-ft)\right)=A\cos (\frac{2\pi }{\lambda }(x-vt))$

এখানে xওy হল তরঙ্গের মান এবং সময় t, এবং A হল তরঙ্গের প্রশস্ততা। এগুলিকে সাধারণত তরঙ্গ সংখ্যা k (তরঙ্গদৈর্ঘ্যের 2π গুণ) এবং কৌণিক কম্পাঙ্ক ω (2π গুণ কম্পাঙ্ক) হিসাবে প্রকাশ করা হয়:

$y(x,t)=A\cos (kx-\omega t)=A\cos (k(x-vt))$

এখানে তরঙ্গদৈর্ঘ্য এবং তরঙ্গবেগ কম্পাঙ্কের সাথে সম্পর্কিত:

$k=\frac{2\pi }{\lambda }=\frac{2\pi f}{v}=\frac{\omega }{v},$

অথবা,

$\lambda =\frac{2\pi }{k}=\frac{2\pi v}{\omega }=\frac{v}{f}.$

উপরে প্রদত্ত দ্বিতীয় ফর্মে, ফেজ টেমপ্লেট:Nowrap প্রায়ই টেমপ্লেট:Nowrap, তরঙ্গসংখ্যা k কে একটি তরঙ্গ ভেক্টর দিয়ে প্রতিস্থাপন করে যা [[3-স্পেসে] একটি সমতল তরঙ্গ এর দিক ও তরঙ্গসংখ্যা নির্দিষ্ট করে। ], অবস্থান ভেক্টর r দ্বারা প্যারামিটারাইজড। সেক্ষেত্রে, তরঙ্গসংখ্যা k, k এর মাত্রা উপরে দেখানো তরঙ্গদৈর্ঘ্যের সাথে এখনও একই সম্পর্কে রয়েছে। v তরঙ্গ ভেক্টর - কে স্কেলার গতি হিসাবে ব্যাখ্যা করা হচ্ছে। প্রথম পর্বে পারস্পরিক তরঙ্গদৈর্ঘ্য ব্যবহার করা ও নির্বিচারে একটি তরঙ্গকে এত সহজে সাধারণীকরণ করা যায় না।

অন্যান্য পর্যায়ের সাইনোসয়েড এবং জটিল সূচকের সাধারণীকরণও সাধারণ; দেখুন সমতল তরঙ্গ। একটি তরঙ্গ বর্ণনা করার সময় সাইন পর্বের পরিবর্তে কোসাইন ফেজ ব্যবহার করায় সাধারণ নিয়মটি এই সত্যের উপর ভিত্তি করে যে কোসাইন হল তরঙ্গের জটিল সূচকের আসল অংশ।

$A{e}^{i(kx-\omega t)}.$

সাধারণ মাধ্যম

ধীরে স্থানান্তরের সাথে একটি মাধ্যমের তরঙ্গদৈর্ঘ্য হ্রাস পায়।

প্রতিসরণ: আলো একটি মাধ্যমে প্রবেশ করার পরে যেখানে এর গতি কম, সেখানে তরঙ্গ দিক পরিবর্তন করে।

একটি প্রিজমের দ্বারা রং পৃথকীকরণ।

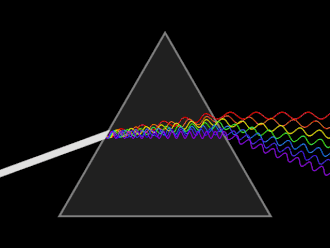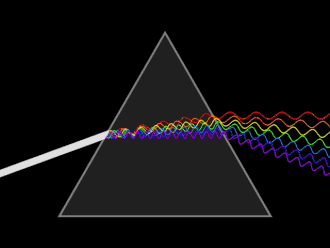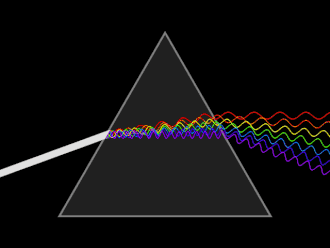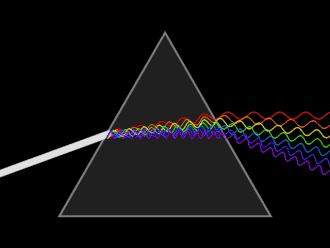
একটি তরঙ্গের গতি নির্ভর করে, এটি যে মাধ্যমে স্থানান্তর করে তার উপর। বিশেষ করে, একটি মাধ্যমের আলোর গতি ভ্যাকুয়াম এর চেয়ে কম, যার অর্থ হল একই কম্পাঙ্ক শূন্যের তুলনায় মাধ্যমের একটি ছোট তরঙ্গদৈর্ঘ্যের সাথে মিলে যাবে, যেমনটি চিত্রে দেখানো হয়েছে।

আলো একটি মাধ্যমে প্রবেশ করার সময় গতির এই পরিবর্তনের কারণে প্রতিসরণ হয়, বা তরঙ্গের দিক পরিবর্তন হয় যা একটি কোণে মাধ্যমের মধ্যে ইন্টারফেসের মুখোমুখি হয়। ইলেক্ট্রোম্যাগনেটিক তরঙ্গ এর জন্য, স্থানান্তরের কোণের এই পরিবর্তনটি স্নেলের সূত্র কে সমার্থ করে।

একটি মাধ্যমের তরঙ্গের বেগ অন্য মাধ্যমের থেকে ভিন্ন হতে পারে না, তবে বেগ সাধারণত তরঙ্গদৈর্ঘ্যের সাথে পরিবর্তিত হয়। ফলস্বরূপ, তরঙ্গ তরঙ্গদৈর্ঘ্যের সাথে ভিন্ন মাধ্যমে প্রবেশ করার সময় দিক পরিবর্তন করে।

ইলেক্ট্রোম্যাগনেটিক তরঙ্গের জন্য একটি মাধ্যমের গতি তার প্রতিসরণ সূচক দ্বারা নিয়ন্ত্রিত হয়।

$v=\frac{c}{n({\lambda }_0)},$

এখানে c হল শূন্যে আলোর গতি এবং n(λ₀) তরঙ্গদৈর্ঘ্য। λ₀-এ মাধ্যমের প্রতিসরণকারী সূচক। যেখানে পরেরটি মাধ্যমের পরিবর্তে ভ্যাকুয়ামে পরিমাপ করা হয়।

$\lambda =\frac{{\lambda }_0}{n({\lambda }_0)}$

যখন ইলেক্ট্রোম্যাগনেটিক বিকিরণের তরঙ্গদৈর্ঘ্য উদ্ধৃত করা হয়, তখন ভ্যাকুয়ামের তরঙ্গদৈর্ঘ্যকে উদ্দেশ্য করা হয় যদি না তরঙ্গদৈর্ঘ্যকে নির্দিষ্টভাবে অন্য কোনো মাধ্যমের তরঙ্গদৈর্ঘ্য হিসাবে চিহ্নিত করা হয়। ধ্বনিবিদ্যায়, যেখানে তরঙ্গের অস্তিত্বের জন্য একটি মাধ্যম অপরিহার্য, সেখানে একটি নির্দিষ্ট মাধ্যমের জন্য তরঙ্গদৈর্ঘ্যের মান দেওয়া হয়।

তরঙ্গদৈর্ঘ্যের সাথে আলোর গতির তারতম্যকে বিচ্ছুরণ বলা হয়, এবং এটি পরিচিত ঘটনার জন্য দায়ী যেখানে আলো একটি প্রিজম দ্বারা উপাদান রঙে বিভক্ত হয়। বিচ্ছেদ ঘটে, যখন প্রিজমের অভ্যন্তরে প্রতিসরাঙ্ক তরঙ্গদৈর্ঘ্যের সাথে পরিবর্তিত হয়, তাই বিভিন্ন তরঙ্গদৈর্ঘ্য প্রিজমের অভ্যন্তরে বিভিন্ন গতিতে স্থানান্তর করে, যার ফলে তারা বিভিন্ন কোণে প্রতিসরিত করে। একটি গাণিতিক সম্পর্ক বর্ণনা করে যে, কীভাবে একটি মাধ্যমের মধ্যে আলোর গতি তরঙ্গদৈর্ঘ্যের সাথে পরিবর্তিত হয়।

আরও কিছু সাধারণ তরঙ্গরূপ

অগভীর পানির উপর পর্যায়ক্রমিক তরঙ্গ

তরঙ্গদৈর্ঘ্যের ধারণাটি প্রায়শই সাইনোসয়েডাল তরঙ্গগুলিতে প্রয়োগ করা হয়, কারণ একটি রৈখিক ব্যবস্থায় সাইনুসয়েড হল অনন্য আকৃতি যা কোন আকৃতির পরিবর্তন ছাড়াই আন্দোলিত করে। তরঙ্গদৈর্ঘ্য (বা বিকল্পভাবে ওয়েভেনম্বার বা তরঙ্গ ভেক্টর) হল মহাকাশের তরঙ্গের একটি বৈশিষ্ট্য, যেটি কার্যত এর কম্পাঙ্কের সাথে সম্পর্কিত, যা সিস্টেমের পদার্থবিদ্যা দ্বারা সীমাবদ্ধ। সাইনুসয়েড হল সবচেয়ে সহজ ট্রাভেলিং ওয়েভ সমাধান, এবং আরও জটিল সমাধানগুলি সুপারপজিশন দ্বারা তৈরি করা যেতে পারে।

বিচ্ছুরণ-মুক্ত এবং অভিন্ন মাধ্যমের বিশেষ ক্ষেত্রে, সাইনোসয়েড ব্যতীত অন্য তরঙ্গগুলি অপরিবর্তিত আকার এবং ধ্রুব বেগের সাথে আন্দোলিত করে। নির্দিষ্ট পরিস্থিতিতে, অপরিবর্তিত আকারের তরঙ্গগুলি অরৈখিক মাধ্যমেও ঘটতে পারে; উদাহরণস্বরূপ, চিত্রটি অগভীর জলে সমুদ্রের উপর তরঙ্গ দেখায় যেগুলির একটি সাইনোসয়েডের তুলনায় তীক্ষ্ণ ক্রেস্ট এবং চ্যাপ্টার তরঙ্গ রয়েছে, যা একটি কনয়েডাল তরঙ্গ, একটি ট্রাভেল তরঙ্গের নামকরণ করা হয়েছে কারণ এটি m-তম ক্রম-এর জ্যাকোবি উপবৃত্তাকার ফাংশন দ্বারা বর্ণনা করা হয়েছে, সাধারণত একে টেমপ্লেট:Nowrap। বৃহৎ-প্রশস্ততা সমুদ্রের তরঙ্গ নির্দিষ্ট আকারের সাথে অপরিবর্তিতভাবে স্থানান্তরিত করতে পারে, কারণ অরৈখিক পৃষ্ঠ-তরঙ্গ মাধ্যমের একটি বৈশিষ্ট্য।

একটি পর্যায়ক্রমিক কিন্তু নন-সাইনুসয়েডাল তরঙ্গরূপের তরঙ্গদৈর্ঘ্য।

যদি একটি ভ্রমণ তরঙ্গের একটি নির্দিষ্ট আকৃতি থাকে যা স্থান বা সময়ে পুনরাবৃত্তি হয় তবে এটি একটি "পর্যায়ক্রমিক তরঙ্গ"। এই ধরনের তরঙ্গগুলিকে কখনও কখনও তরঙ্গদৈর্ঘ্য হিসাবে বিবেচনা করা হয় যদিও তারা সাইনোসাইডাল নয়। চিত্রে দেখানো হয়েছে, তরঙ্গদৈর্ঘ্য তরঙ্গরূপের ধারাবাহিক সংশ্লিষ্ট বিন্দুগুলির মধ্যে পরিমাপ করা হয়।

তরঙ্গ প্যাকেট

একটি প্রচার তরঙ্গ প্যাকেট

স্থানীয়কৃত তরঙ্গ প্যাকেট, তরঙ্গ ক্রিয়ার "বিস্ফোরণ" যেখানে প্রতিটি তরঙ্গ প্যাকেট একক হিসাবে ভ্রমণ করে, পদার্থবিজ্ঞানের অনেক ক্ষেত্রে প্রয়োগ খুঁজে পায়। একটি তরঙ্গ প্যাকেটে একটি খাম থাকে যা তরঙ্গের সামগ্রিক প্রশস্ততা বর্ণনা করে; খামের মধ্যে, সংলগ্ন শিখর বা খাদের মধ্যে দূরত্বকে কখনও কখনও স্থানীয় তরঙ্গদৈর্ঘ্য বলা হয়। একটি উদাহরণ চিত্রে দেখানো হয়েছে। সাধারণভাবে, তরঙ্গ প্যাকেটের খাম উপাদান তরঙ্গ থেকে ভিন্ন গতিতে চলে। ফুরিয়ার বিশ্লেষণ ব্যবহার করে, তরঙ্গ প্যাকেটগুলি বিভিন্ন তরঙ্গ সংখ্যা বা তরঙ্গদৈর্ঘ্যের সাইনোসয়েডাল তরঙ্গের অসীম সমষ্টি (বা অখণ্ড) বিশ্লেষণ করা যেতে পারে।লুইস ডি ব্রোগলি অনুমান করেছিলেন যে মোমেন্টাম p এর একটি নির্দিষ্ট মান সহ সমস্ত কণার একটি তরঙ্গদৈর্ঘ্য λ = h/p আছে, যেখানে h হল প্ল্যাঙ্কের ধ্রুবক । এই হাইপোথিসিসটি ছিল কোয়ান্টাম মেকানিক্স এর ভিত্তিতে। আজকাল, এই তরঙ্গদৈর্ঘ্যকে ডি ব্রোগলি তরঙ্গদৈর্ঘ্য বলা হয়। উদাহরণস্বরূপ, একটি CRT ডিসপ্লেতে ইলেক্ট্রনগুলির একটি ডি ব্রগলি তরঙ্গদৈর্ঘ্য প্রায় 10⁻¹³ মি। এই ধরনের একটি কণা সমস্ত মহাকাশে ছড়িয়ে পড়ার জন্য তরঙ্গ ফাংশন প্রতিরোধ করার জন্য, ডি ব্রোগলি মহাকাশে স্থানীয়করণ করা কণাগুলিকে উপস্থাপন করার জন্য তরঙ্গ প্যাকেট ব্যবহার করার প্রস্তাব করেছিলেন। তরঙ্গ প্যাকেটের স্থানিক বিস্তার, এবং প্যাকেট তৈরিকারী সাইনোসয়েডগুলির তরঙ্গ সংখ্যা বিস্তার কণার অবস্থান এবং ভরবেগের অনিশ্চয়তার সাথে মিলে যায়, যার পণ্যটি হেইজেনবার্গ অনিশ্চয়তা নীতি দ্বারা আবদ্ধ। ।

হস্তক্ষেপ এবং বিভাজন

ডাবল-স্লিট হস্তক্ষেপ

দুটি স্লিটের মধ্য দিয়ে আলো যাওয়ার জন্য একটি পর্দায় আলোর তীব্রতার একটি প্যাটার্ন। ডানদিকের লেবেল দুটি স্লিট থেকে পথের দৈর্ঘ্যের পার্থক্য নির্দেশ করে, যা এখানে পয়েন্ট উৎস হিসাবে আদর্শ ধরা হয়েছে।

যখন সাইন তরঙ্গরূপ পরস্পর যোগ হয়, তখন তারা একে অপরকে শক্তিশালী করতে পারে (গঠনমূলক হস্তক্ষেপ) বা তাদের আপেক্ষিক পর্যায়ের উপর নির্ভর করে একে অপরকে (ধ্বংসাত্মক হস্তক্ষেপ) বাতিল করতে পারে। এই ঘটনাটি ইন্টারফেরোমিটার এ ব্যবহৃত হয়। একটি সাধারণ উদাহরণ হল ইয়ং একটি পরীক্ষা করেছিলেন যে, আলো দুটি স্লিট এর মধ্য দিয়ে যায়। চিত্রে দেখানো হয়েছে, আলো দুটি স্লিটের মধ্য দিয়ে যায় এবং একটি পর্দায় জ্বলে। পর্দার একটি অবস্থানে আলোর পথ দুটি স্লিটের জন্য আলাদা, এবং পর্দার সাথে পথটি যে কোণ তৈরি করে তার উপর সেটি নির্ভর করে। যদি আমরা মনে করি স্লিটগুলি থেকে স্ক্রীনটি যথেষ্ট দূরে (অর্থাৎ, স্লিট সেপারেশন d-এর তুলনায় s বড়) তাহলে পথগুলি প্রায় সমান্তরাল, এবং পথের পার্থক্য কেবল d sinθ। তদনুসারে, গঠনমূলক হস্তক্ষেপের শর্ত হল:

$d\sin \theta =m\lambda ,$

এখানে m একটি পূর্ণসংখ্যা, এবং বিনাশক হস্তক্ষেপের জন্য হল:

$d\sin \theta =(m+1/2)\lambda .$

এইভাবে, আলোর তরঙ্গদৈর্ঘ্য জানা থাকলে, হস্তক্ষেপ প্যাটার্ন বা ফ্রিঞ্জ থেকে এবং তদ্বিপরীত থেকে চেরা বিচ্ছেদ নির্ধারণ করা যেতে পারে।

একাধিক স্লিটের জন্য, প্যাটার্ন হয়

$I_q=I_1{\sin }^2\left(\frac{q\pi g\sin \alpha }{\lambda }\right)/{\sin }^2\left(\frac{\pi g\sin \alpha }{\lambda }\right),$

এখানে q হল স্লিটের সংখ্যা, এবং g হল গ্রেটিং ধ্রুবক। প্রথম ফ্যাক্টর, I₁ হল একক-স্লিটের ফলাফল, যা আরও দ্রুত হারে দ্বিতীয় ফ্যাক্টরকে পরিবর্তন করে যা স্লিটের সংখ্যা এবং তাদের ব্যবধানের উপর নির্ভর করে।

হস্তক্ষেপের প্রভাব হল, আলোকে পুনঃবন্টন করা, তাই আলোর মধ্যে থাকা শক্তির পরিবর্তন হয় না।

একক-স্লিট বিচ্ছুরণ

একটি ডাবল স্লিটের ডিফ্র্যাকশন প্যাটার্নে একটি একক-স্লিট আছে খাম।

ডাবল-স্লিট পরীক্ষার জন্য উপরে ব্যবহৃত পথের পার্থক্য এবং গঠনমূলক বা ধ্বংসাত্মক হস্তক্ষেপের ধারণাটি স্ক্রিনে আটকানো আলোর একক স্লিটের প্রদর্শনের ক্ষেত্রেও প্রযোজ্য। এই হস্তক্ষেপের প্রধান ফলাফল হল সরু স্লিট থেকে আলোকে স্ক্রিনে একটি বিস্তৃত চিত্রে ছড়িয়ে দেওয়া। তরঙ্গ শক্তির এই বন্টনকে বলা হয় বিবর্তন।

$S(u)={\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}}^2(u)={\left(\frac{\sin \pi u}{\pi u}\right)}^2;$  with  $u=\frac{xL}{\lambda R},$

এখানে L হল স্লিট প্রস্থ, R হল স্লিট থেকে প্যাটার্নের দূরত্ব (স্ক্রীনে) এবং λ হল আলোর তরঙ্গদৈর্ঘ্য। ফাংশন S-এ শূন্য রয়েছে। যেখানে u একটি অ-শূন্য পূর্ণসংখ্যা, যেখানে x এর মান তরঙ্গদৈর্ঘ্যের বিচ্ছেদ অনুপাতে রয়েছে।

উপ তরঙ্গদৈর্ঘ্য

"উপ তরঙ্গদৈর্ঘ্য" শব্দটি একটি বস্তুকে বর্ণনা করতে ব্যবহৃত হয় যার সাথে বস্তুটি যোগাযোগ করে।তরঙ্গের দৈর্ঘ্যের চেয়ে এক বা একাধিক উপ তরঙ্গদৈর্ঘ্যের মাত্রা ছোট। উদাহরণ স্বরূপ, "সাবওয়েভলেন্থ-ডাইয়ামিটার অপটিক্যাল ফাইবার" শব্দের অর্থ হল একটি অপটিক্যাল ফাইবার এর ব্যাস, অপটিক্যাল ফাইবারের মাধ্যমে স্থানান্তরিত আলোর তরঙ্গদৈর্ঘ্যের চেয়ে কম।

একটি উপ তরঙ্গদৈর্ঘ্য কণা হল আলোর তরঙ্গদৈর্ঘ্যের চেয়ে ছোট একটি কণা যার সাথে এটি যোগাযোগ করে (দেখুন Rayleigh স্ক্যাটারিং)। উপ তরঙ্গদৈর্ঘ্যের অ্যাপারচারগুলি আলোর তরঙ্গদৈর্ঘ্যের চেয়ে ছোট গর্ত যা তাদের মাধ্যমে স্থানান্তরিত হয়। এই ধরনের কাঠামোর মতো অসাধারণ অপটিক্যাল ট্রান্সমিশন, এবং শূন্য-মোড ওয়েভগাইড, ফটোনিক্স এর অন্যান্য ক্ষেত্রগুলির মধ্যে অ্যাপ্লিকেশন রয়েছে।

উপ তরঙ্গদৈর্ঘ্য এমন একটি ঘটনাকেও উল্লেখ করতে পারে যা উপ তরঙ্গদৈর্ঘ্যের বস্তুর সাথে জড়িত। উদাহরণস্বরূপ, সাবওয়েভলেন্থ ইমেজিং।

কৌণিক তরঙ্গদৈর্ঘ্য

তরঙ্গদৈর্ঘ্য, কৌণিক তরঙ্গদৈর্ঘ্য এবং অন্যান্য তরঙ্গ বৈশিষ্ট্যের মধ্যে সম্পর্ক।

তরঙ্গদৈর্ঘ্যের সাথে সম্পর্কিত একটি রাশি হলো কৌণিক তরঙ্গদৈর্ঘ্য (এছাড়াও হ্রাসিত তরঙ্গদৈর্ঘ্য নামে পরিচিত), সাধারণত ƛ (ল্যাম্বদা-বার) দ্বারা প্রতীকী। এটি 2π (ƛ = λ/2π) একটি গুণনীয়ক দ্বারা "নিয়মিত" তরঙ্গদৈর্ঘ্য "হ্রাস" এর সমান। এটি সাধারণত কোয়ান্টাম মেকানিক্সের সম্মুখীন হয়, যেখানে এটি হ্রাসিত প্লাঙ্ক ধ্রুবক (প্রতীক ħ, h-বার) এবং কৌণিক কম্পাঙ্ক (প্রতীক ω) বা কৌণিক তরঙ্গ সংখ্যা (প্রতীক k)।

আরও দেখুন

• তরঙ্গ
• দৈর্ঘ্য
• প্রিজম
• অনুদৈর্ঘ্য তরঙ্গ
• আড় তরঙ্গ

বহিঃসংযোগ

• অবস্থান্তর: তরঙ্গদৈর্ঘ্য থেকে কম্পাঙ্ক এবং তদ্বিপরীত - শব্দ তরঙ্গ এবং রেডিও তরঙ্গ টেমপ্লেট:ওয়েব আর্কাইভ
• তরঙ্গদৈর্ঘ্য সহ কিছু শব্দের উপর 14-16 বছরের জন্য শিক্ষাদানের সংস্থান টেমপ্লেট:ওয়েব আর্কাইভ
• তরঙ্গদৈর্ঘ্য অনুযায়ী ওয়েব রঙে প্রদর্শিত দৃশ্যমান ইলেক্ট্রোম্যাগনেটিক বর্ণালী