ত্রিকোণমিতি

ত্রিকোণমিতি গণিতের একটি শাখা, যাতে ত্রিভুজের কোণ, বাহু ও তাদের মধ্যকার সম্পর্ক ব্যবহার করে বিভিন্ন সমস্যার সমাধান করা হয়। ত্রিকোণমিতি শব্দের ইংরেজি প্রতিশব্দ হচ্ছে Trigonometry। এই শব্দটি আবার গ্রিক শব্দ trigōnon (ত্রিভুজ) এবং metron (পরিমাপ) থেকে উদ্ভূত।

বিশেষ করে ত্রিভুজের তিনটি কোণের অপেক্ষকগুলো নানা পরিমাপের কাজে লাগানো যায়। ত্রিভুজের প্রতিটি কোণের ছয় প্রকারের অপেক্ষক বা ফাংশন থাকে। যথা সাইন (sine), কোসাইন (cosine), ট্যাঞ্জেন্ট (tangent), কোট্যাঞ্জেণ্ট (cotangent), সেক্যাণ্ট (secant) এবং কোসেক্যাণ্ট (cosecant)। এগুলো ব্যবহার করে ত্রিভুজের কোণ ও বাহুর দৈর্ঘ্য হিসাব করা হয়।

ত্রিকোণমিতির অপেক্ষকগুলো বেশ গুরুত্বপূর্ণ। কারণ এগুলোর মাধ্যমে বিভিন্ন মানের পাল্লার প্রতিরূপ দেয়া যায় বা বারবার পুনরাবৃত্ত হয়। এগুলো পুনরাবৃত্ত প্রতিভাসের প্রতিরূপে, যেমন সরল দোলকের গতি অথবা পরিবর্তী তড়িৎ প্রবাহের বিশ্লেষণে উদ্ভূত হয়। ত্রিকোণমিতির ব্যবহার করে এক বিশাল ক্ষেত্রফলের জালিকা পাওয়া যায় যা সাধারণ পরিমাপ পদ্ধতি ব্যবহার করে মাপা যায় না।

ইতিহাস

টেমপ্লেট:মূল ত্রিকোণমিতির জন্ম প্রাচীন মিশরে হলেও এর আদি উদ্ভাবক একজন গ্রিক জ্যোতির্বিদ যার নাম হিপারকাস। খ্রিষ্টপূর্ব দ্বিতীয় শতকে গ্রিক হিপারকাস গ্রহ-নক্ষত্র ও তাদের মধ্যবর্তী বেগ এবং দুরত্ব নির্ণয় ও বিচার করতে গিয়ে এই বিদ্যার চর্চা শুরু করেন। তিনি কাজ করতেন আলেকজান্দ্রিয়ার একটি জাদুঘরে। তবে আমরা বর্তমান যুগে ‘থেটা’, ‘সাইন’, ‘কস’, ‘কোসাইন’, ‘কোসেক’ ইত্যাদি দিয়ে যে ত্রিকোণমিতি করে থাকি তার উদ্ভাবক মুসলিম গণিতবিদেরা। নবম খ্রিষ্টাব্দে আবু আবদুল্লাহ আল-বাতানি, হাবাস আল-হাসিব ও আবুল ওয়াফা আল-বুজানি নামের তিন গণিতবিদের যৌথ উদ্যোগের ফসল আধুনিক ত্রিকোণমিতি। তবে তারা গ্রিক জ্যোতির্বিদ হিপারকাসের মূল ধারণার ওপর ভিত্তি করেই এ বিষয়টিকে আরও আধুনিক করে গড়ে তুলেছিলেন।

ত্রিকোণমিতিক অনুপাত

একটি কোণ θ-এর যেকোন ত্রিকোণমিতীয় ফাংশনকে "O" কেন্দ্রবিশিষ্ট একটি বৃত্তের মাধ্যমে প্রকাশ করা যেতে পারে।

যদি ত্রিভুজের একটি কোণ সমকোণ হয় এবং অপর কোণের মান জানা থাকে তবে তৃতীয় কোণের পরিমাপ নির্ণয় করা যায়। এবার আমরা জানি ত্রিভুজের তিন কোনের সমষ্টি ১৮০ ডিগ্রি। কাজেই সমকোণ বাদে বাকি কোণদ্বয়ের সমষ্টি ৯০ ডিগ্রি। তিনটি কোণের পরিমাপ জানা থাকলে ত্রিভুজের বাহুত্রয়ের পরিমাপের নির্ণয় করা যায়। আর যে কোনো এক বাহুর দৈর্ঘ্য জানা থাকলে বাকি বাহুর দৈর্ঘ্যও জানা যায়। এই অনুপাতগুলো জানা যায় কোন θ এর ত্রিকোণোমিতীয় অপেক্ষক বা ফাংশন থেকে।

চিত্রের ত্রিভুজে: টেমপ্লেট:Math টেমপ্লেট:Math এবং টেমপ্লেট:Math

• সাইন: এটি ত্রিভুজের লম্ব ও অতিভুজের অনুপাত প্রকাশ করে

$\sin A=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{a}{c}.$

• কোসাইন: এটি ত্রিভুজের ভূমি ও অতিভুজের অনুপাত প্রকাশ করে

$\cos A=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{b}{c}.$

• ট্যানজেন্ট: এটি ত্রিভুজের লম্ব ও ভূমির অনুপাত প্রকাশ করে

$\tan A=\frac{\text{opposite}}{\text{adjacent}}=\frac{a}{b}=\frac{a/c}{b/c}=\frac{\sin A}{\cos A}.$

এই ফাংশনগুলোর গুণোত্তর বিপরীত ফাংশনগুলোকে যথাক্রমে কোসেকেন্ট (cosec বা csc), সেকেন্ট (sec) এবং কোট্যানজেন্ট (cot) বলা হয়।

$\csc A=\frac{1}{\sin A}=\frac{\text{hypotenuse}}{\text{opposite}}=\frac{c}{a},$

$\sec A=\frac{1}{\cos A}=\frac{\text{hypotenuse}}{\text{adjacent}}=\frac{c}{b},$

$\cot A=\frac{1}{\tan A}=\frac{\text{adjacent}}{\text{opposite}}=\frac{\cos A}{\sin A}=\frac{b}{a}.$

একক বৃত্ত ও সাধারণ ত্রিকোণমিতিক মানসমূহ

একক বৃত্তের সাহায্যে সংজ্ঞায়িত θ কোণের সাইন ও কোসাইন অনুপাত

ফাংশন	0°(0)	30°$(\pi /6)$	45°$(\pi /4)$	90°$(\pi /3)$	120°$(\pi /2)$	180°$(2\pi /3)$	270°$(3\pi /4)$	360°$(5\pi /6)$	$(\pi )$
সাইন	0	$1/2$	$\sqrt{2}/2$	$\sqrt{3}/2$	1	$\sqrt{3}/2$	$\sqrt{2}/2$	$1/2$	0
কোসাইন	1	$\sqrt{3}/2$	$\sqrt{2}/2$	$1/2$	0	$-1/2$	$-\sqrt{2}/2$	$-\sqrt{3}/2$	-1
ট্যানজেন্ট	0	$\sqrt{3}/3$	$1$	$\sqrt{3}$	অসংজ্ঞায়িত	$-\sqrt{3}$	$-1$	$-\sqrt{3}/3$	0
সেকেন্ট	1	$2\sqrt{3}/3$	$\sqrt{2}$	$2$	অসংজ্ঞায়িত	$-2$	$-\sqrt{2}$	$-2\sqrt{3}/3$	-1
কোসেকেন্ট	অসংজ্ঞায়িত	$2$	$\sqrt{2}$	$2\sqrt{3}/3$	1	$2\sqrt{3}/3$	$\sqrt{2}$	$2$	অসংজ্ঞায়িত
কোট্যানজেন্ট	অসংজ্ঞায়িত	$\sqrt{3}$	$1$	$\sqrt{3}/3$	0	$-\sqrt{3}/3$	$-1$	$-\sqrt{3}$	অসংজ্ঞায়িত

বাস্তব ও জটিল চলকের ত্রিকোণমিতিক ফাংশন

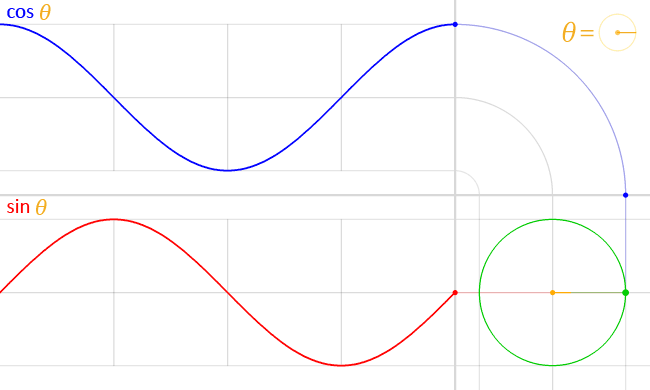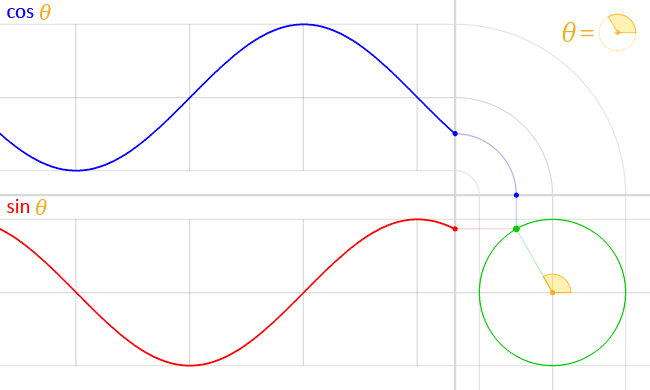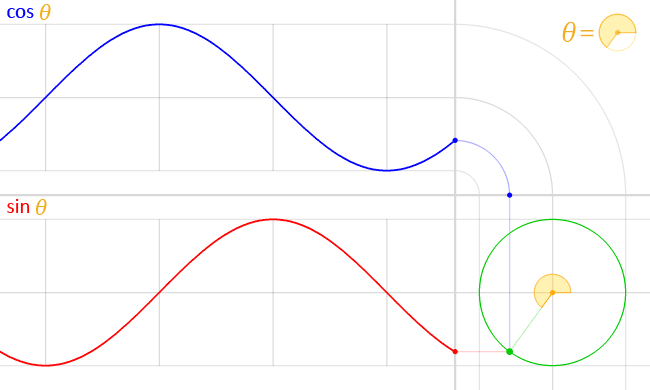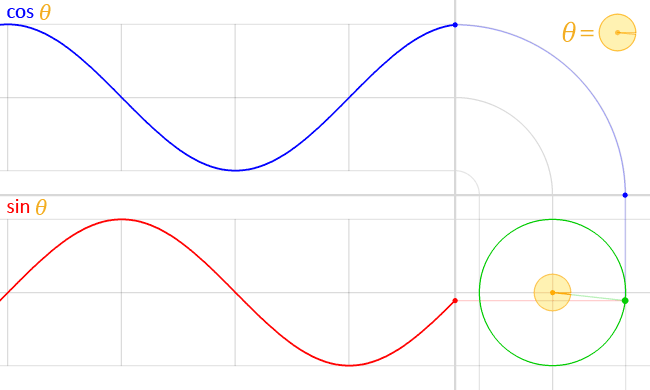
ত্রিকোণমিতিক ফাংশনের লেখচিত্র

নিচের ছকে ৬টি প্রধান ত্রিকোণমিতিক ফাংশনের রেখচিত্রের বৈশিষ্ট্য দেওয়া হলো:

ফাংশন	পর্যায়	ডোমেন	রেঞ্জ	লেখচিত্র
সাইন	$2\pi$	$(-\mathrm{\infty },\mathrm{\infty })$	$[-1,1]$
কোসাইন	$2\pi$	$(-\mathrm{\infty },\mathrm{\infty })$	$[-1,1]$
ট্যানজেন্ট	$\pi$	$x\ne \pi /2+n\pi$	$(-\mathrm{\infty },\mathrm{\infty })$
সেকেন্ট	$2\pi$	$x\ne \pi /2+n\pi$	$(-\mathrm{\infty },-1]\cup [1,\mathrm{\infty })$
কোসেকেন্ট	$2\pi$	$x\ne n\pi$	$(-\mathrm{\infty },-1]\cup [1,\mathrm{\infty })$
কোট্যানজেন্ট	$\pi$	$x\ne n\pi$	$(-\mathrm{\infty },\mathrm{\infty })$

বিপরীত ত্রিকোণমিতিক ফাংশন

নাম	রাশি	সংজ্ঞা	বাস্তব মানের জন্য x-এর ডোমেন	রেঞ্জ (রেডিয়ান)	রেঞ্জ (ডিগ্রি)
arcsine	y = টেমপ্লেট:Math বা y = sinটেমপ্লেট:Sup(x)	x = টেমপ্লেট:Math	−১ ≤ x ≤ ১	−টেমপ্লেট:Sfrac ≤ y ≤ টেমপ্লেট:Sfrac	−৯০° ≤ y ≤ ৯০°
arccosine	y = টেমপ্লেট:Math বা y = cosটেমপ্লেট:Sup(x)	x = টেমপ্লেট:Math	−১ ≤ x ≤ ১	০ ≤ y ≤ টেমপ্লেট:Pi	০° ≤ y ≤ ১৮০°
arctangent	y = টেমপ্লেট:Math বা y = tanটেমপ্লেট:Sup(x)	x = টেমপ্লেট:Math	সকল বাস্তব সংখ্যা	−টেমপ্লেট:Sfrac < y < টেমপ্লেট:Sfrac	−৯০° < y < ৯০°
arccotangent	y = টেমপ্লেট:Math বা y = cotটেমপ্লেট:Sup(x)	x = টেমপ্লেট:Math	সকল বাস্তব সংখ্যা	০ < y < টেমপ্লেট:Pi	০° < y < ১৮০°
arcsecant	y = টেমপ্লেট:Math বা y = secটেমপ্লেট:Sup(x)	x = টেমপ্লেট:Math	x ≤ −১ বা ১ ≤ x	০ ≤ y < টেমপ্লেট:Sfrac বা টেমপ্লেট:Sfrac < y ≤ টেমপ্লেট:Pi	০° ≤ y < ৯০° বা ৯০° < y ≤ ১৮০°
arccosecant	y = টেমপ্লেট:Math বা y = cosecটেমপ্লেট:Sup(x)	x = টেমপ্লেট:Math	x ≤ −১ বা ১ ≤ x	−টেমপ্লেট:Sfrac ≤ y < ০ বা ০ < y ≤ টেমপ্লেট:Sfrac	−৯০° ≤ y < ০° বা ০° < y ≤ ৯০°

অভেদসমূহ

ত্রিভুজ সম্পর্কিত অভেদ

সাইন সূত্র

সাইন নিয়ম অনুসারে যে কোনো ত্রিভুজে:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R=\frac{abc}{2\mathrm{\Delta }}$

যেখানে $\mathrm{\Delta }$ হচ্ছে ত্রিভুজটির ক্ষেত্রফল এবং R হল ত্রিভুজটির পরিবৃত্তের ব্যাসার্ধ।

$R=\frac{abc}{\sqrt{(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}$

কোসাইন সূত্র

কোসাইন নিয়ম (বা কস সূত্র) আসলে পিথাগোরাসের সূত্রের সম্প্রসারিত রূপ। এ সূত্র অনুসারে:

$c^2=a^2+b^2-2ab\cos C$

বা, $\cos C=\frac{a^2+b^2-c^2}{2ab}$

ট্যাঞ্জেণ্টের সূত্র

$\frac{a-b}{a+b}=\frac{\tan [\frac{1}{2}(A-B)]}{\tan [\frac{1}{2}(A+B)]}$

ক্ষেত্রফল

দুটি বাহু a ও b এবং এদের মধ্যবর্তী কোণ C হলে ত্রিভুজের ক্ষেত্রফল কোণের সাইন এবং বাহুদ্বয়ের গুণফলের অর্ধেক।

$\text{Area}=\mathrm{\Delta }=\frac{1}{2}ab\sin C$

হিরনের সূত্রের সাহায্যেও ত্রিভুজের ক্ষেত্রফল নির্ণয় করা যায়। ত্রিভুজের তিন বাহুর দৈর্ঘ্য যথাক্রমে a, b ও c হলে ত্রিভুজের অর্ধপরিসীমা =

$s=\frac{1}{2}(a+b+c),$

সুতরাং ত্রিভুজের ক্ষেত্রফল =

$\text{Area}=\mathrm{\Delta }=\sqrt{s(s-a)(s-b)(s-c)}=\frac{abc}{4R}$

যেখানে R হল ত্রিভুজটির পরিবৃত্তের ব্যাসার্ধ।

ত্রিকোণমিতিক অভেদ

পিথাগোরাসীয় অভেদ

নিচের ত্রিকোণমিতিক অভেদগুলো পিথাগোরাসের সূত্রের সাথে সম্পর্কিত এবং যে কোনো মান গ্রহণ করতে পারে।

${\sin }^{2}A+{\cos }^{2}A=1$

${\tan }^{2}A+1={\sec }^{2}A$

${\cot }^{2}A+1={\csc }^{2}A$

অয়লারের সূত্র

টেমপ্লেট:মূল নিবন্ধ$\sin x=\frac{e^{ix}-e^{-ix}}{2i},\cos x=\frac{e^{ix}+e^{-ix}}{2},\tan x=\frac{i(e^{-ix}-e^{ix})}{e^{ix}+e^{-ix}}$

গ্রন্থপঞ্জি

• টেমপ্লেট:বই উদ্ধৃতি
• টেমপ্লেট:বই উদ্ধৃতি
• টেমপ্লেট:বই উদ্ধৃতি

বহিঃসংযোগ

• টেমপ্লেট:ওয়েব উদ্ধৃতি
• টেমপ্লেট:ওয়েব উদ্ধৃতি
• টেমপ্লেট:ওয়েব উদ্ধৃতি