ডপলার ক্রিয়া

উৎসের গতির কারণে তরঙ্গদৈর্ঘ্যের পরিবর্তন।

একটি গাড়ি কাছে আসার সময় ডপলার ক্রিয়া কিভাবে পিচের পরিবর্তন করে তা একটি অ্যানিমেশনের মাধ্যমে দেখানো হয়েছে। লাল বৃত্তটি শব্দ তরঙ্গকে প্রতিনিধিত্ব করে।

ডপলার প্রভাব বা ডপলার শিফট (অথবা শুধু ডপলার) হল তরঙ্গের উৎসের সাপেক্ষে একটি পর্যবেক্ষকের গতিশীলতার সাথে সম্পর্কিত একটি তরঙ্গের কম্পাঙ্কের আপাত পরিবর্তন। অস্ট্রিয়ান পদার্থবিদ ক্রিশ্চিয়ান ডপলারের নামানুসারে এই ক্রিয়ার নামকরণ করা হয়েছে। তিনি ১৮৪২ সালে ঘটনাটি বর্ণনা করেছিলেন।

ডপলার ক্রিয়ার একটি সাধারণ উদাহরণ হল হর্ন বাজানো একটি গাড়ির কাছে আসা এবং পর্যবেক্ষকের কাছ থেকে সরে যাবার সময় পিচের পরিবর্তন। এক্ষেত্রে নির্গত কম্পাঙ্কের তুলনায় প্রাপ্ত কম্পাঙ্ক কাছে আসার সময় বেশি, পাশ কাটিয়ে যাওয়ার মুহূর্তে একই রকম এবং প্রত্যাবর্তনের কম বলে মনে হয়।

ডপলার প্রভাবের কারণ হল যে তরঙ্গের উৎস পর্যবেক্ষকের দিকে অগ্রসর হবার সময় প্রতিটি ধারাবাহিক তরঙ্গ শীর্ষ আগের তরঙ্গের শীর্ষের চেয়ে পর্যবেক্ষকের কাছাকাছি অবস্থান থেকে নির্গত হয়। তাই প্রতিটি তরঙ্গ পূর্ববর্তী তরঙ্গের তুলনায় পর্যবেক্ষকের কাছে পৌঁছাতে কিছুটা কম সময় নেয়। ফলে পর্যবেক্ষকের কাছে ক্রমাগত তরঙ্গ শীর্ষের আগমনের মধ্যে সময় কমে যায় ও ফলে কম্পাঙ্ক বৃদ্ধি পায়। এতে ভ্রমণ করার সময় পাশাপাশি অবস্থিত তরঙ্গের মধ্যে দূরত্ব হ্রাস পায়।

বিপরীতভাবে যদি তরঙ্গের উৎস পর্যবেক্ষক থেকে দূরে সরে যায়, প্রতিটি তরঙ্গ পূর্ববর্তী তরঙ্গের চেয়ে পর্যবেক্ষক থেকে দূরের অবস্থান থেকে নির্গত হয়। তাই ধারাবাহিক তরঙ্গের মধ্যে সময় বৃদ্ধি পায় ও কম্পাঙ্ক হ্রাস করে। ফলে ভ্রমণ করার সময় পাশাপাশি অবস্থিত তরঙ্গের মধ্যে দূরত্ব বৃদ্ধি পায়।

যে তরঙ্গগুলি একটি মাধ্যমে সঞ্চালিত হয়, যেমন শব্দ তরঙ্গের জন্য, পর্যবেক্ষকের বেগ এবং উৎসের বেগ সেই মাধ্যমের সাথে আপেক্ষিক হয়, যেখানে তরঙ্গগুলি প্রেরণ করা হয়। মোট ডপলার প্রভাব তাই উৎসের গতি, পর্যবেক্ষকের গতি, মাধ্যমের গতি বা এর যেকোন সংমিশ্রণের ফলে হতে পারে। ইলেক্ট্রোম্যাগনেটিক ওয়েভ বা মহাকর্ষীয় তরঙ্গের মতো ভ্যাকুয়ামে সঞ্চালিত তরঙ্গগুলির জন্য শুধুমাত্র পর্যবেক্ষক এবং উৎসের মধ্যে বেগের পার্থক্য বিবেচনা করা প্রয়োজন। যদি এই আপেক্ষিক বেগ আলোর বেগের তুলনায় নগণ্য না হয় তবে আরও জটিল আপেক্ষিক ডপলার প্রভাব দেখা দেয়।

ইতিহাস

উট্রেচট-এর একটি দেয়ালে বুইস ব্যালট (১৮৪৫) দ্বারা পরীক্ষা চিত্রিত করা হয়েছে (২০১৯)

১৮৪২ সালে ডপলার প্রথম তার গ্রন্থে (Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels" -আকাশের বাইনারি তারা এবং কিছু অন্যান্য নক্ষত্রের রঙিন আলোতে) এই প্রভাবের প্রস্তাব করেছিলেন। ১৮৪৫ সালে বুইস ব্যালট হাইপোথিসিসটি শব্দ তরঙ্গের জন্য পরীক্ষা করেছিলেন। তিনি প্রমাণ করেন যে যখন শব্দের উৎস তার কাছে আসে তখন শব্দের পিচ নির্গত কম্পাঙ্কের চেয়ে বেশি ছিল এবং যখন শব্দের উৎস তার থেকে দূরে সরে যায় তখন পিচ নির্গত কম্পাঙ্কের চেয়ে কম ছিল। হিপ্পোলাইট ফিজেউ ১৮৪৮ সালে ইলেক্ট্রোম্যাগনেটিক তরঙ্গে একই ঘটনাটি স্বাধীনভাবে আবিষ্কার করেছিলেন (একারণে ফ্রান্সে, প্রভাবটিকে কখনও কখনও "এফেট ডপলার-ফিজেউ" বলা হয় তবে ডপলারের প্রস্তাবের ছয় বছর পরে ফিজেউর আবিষ্কারের কারণে এই নামটি গৃহীত হয়নি)। ব্রিটেনে, জন স্কট রাসেল ডপলার প্রভাব (১৮৪৮) নিয়ে একটি পরীক্ষামূলক গবেষণা করেন।

সাধারণ

চিরায়ত পদার্থবিজ্ঞানে, যেখানে মাধ্যমের সাপেক্ষে উৎসের গতি এবং গ্রাহকের গতি মাধ্যমটির তরঙ্গের গতির চেয়ে কম, সেখানে পর্যবেক্ষণকৃত কম্পাঙ্কের মধ্যে সম্পর্ক $f$ এবং নির্গত কম্পাঙ্ক $f_{\text{0}}$ দ্বারা প্রাকাশ করা হয়:$$f=\left(\frac{c\pm v_{\text{r}}}{c\pm v_{\text{s}}}\right)f_0$$যেখানে,

• $c$ মাধ্যমে তরঙ্গ সঞ্চালনের গতি;
• $v_{\text{r}}$ মাধ্যম সাপেক্ষে গ্রাহকের গতি, এর সাথে যোগ করা হয় $c$ যদি গ্রাহক উৎসের দিকে অগ্রসর হয়, বিয়োগ করা হয় যদি গ্রাহক উৎস থেকে দূরে সরে যায়;
• $v_{\text{s}}$ মাধ্যমের সাপেক্ষে উৎসের গতি, যোগ করা হয় $c$ উৎস যদি গ্রাহক থেকে দূরে সরে যায়, বিয়োগ করা হয় যদি উৎসটি গ্রাহকের দিকে যায়।

মনে রাখা জরুরি যে, এই সম্পর্কটি থেকে জানা যায় যে উৎস বা গ্রাহক একে অন্য থেকে দূরে সরে গেলে কম্পাঙ্ক হ্রাস পাবে।

একইভাবে উৎসটি পর্যবেক্ষকের সরাসরি কাছে আসছে বা দূরে সরে যাচ্ছে ধারণার অধীনে:$$\frac{f}{v_{wr}}=\frac{f_0}{v_{ws}}=\frac{1}{\lambda }$$যেখানে,

• $v_{wr}$ গ্রাহকের সাপেক্ষে তরঙ্গের গতি;
• $v_{ws}$ উৎসের সাপেক্ষে তরঙ্গের গতি;
• $\lambda$ তরঙ্গদৈর্ঘ্য।

যদি উৎসটি একটি কোণে পর্যবেক্ষকের কাছে আসে (কিন্তু এখনও একটি ধ্রুব গতির সাথে), পর্যবেক্ষণকৃত প্রথম শোনা কম্পাঙ্ক বস্তু নির্গত কম্পাঙ্কের চেয়ে বেশি হয়। এরপরে পর্যবেক্ষকের কাছাকাছি আসার সাথে সাথে পর্যবেক্ষকের কম্পাঙ্ক হ্রাস পায়। যখন এটি আপেক্ষিক গতির সাথে লম্ব দিক থেকে আসে তখন সমতার মাধ্যমে (এবং নিকটতম অভিমুখ বিন্দুতে নির্গত হয়; কিন্তু যখন তরঙ্গটি প্রাপ্ত হয়, উৎস এবং পর্যবেক্ষক আর তাদের নিকটতম অবস্থানে থাকবে না) এবং পর্যবেক্ষকের কাছ থেকে সরে যাওয়ার সাথে সাথে ক্রমাগত হ্রাস পায়। যখন পর্যবেক্ষক বস্তুর পথের খুব কাছাকাছি থাকে, তখন উচ্চ থেকে নিম্ন কম্পাঙ্কে রূপান্তর খুব আকস্মিক হয়। যখন পর্যবেক্ষক বস্তুর থেকে দূরে থাকে, তখন উচ্চ থেকে নিম্ন কম্পাঙ্কে রূপান্তর ধীরে ধীরে হয়।

যদি $v_{\text{s}}$ এবং $v_{\text{r}}$ তরঙ্গের গতির তুলনায় ছোট থাকে, তখন পর্যবেক্ষিত কম্পাঙ্কের মধ্যে সম্পর্ক $f$ এবং নির্গত কম্পাঙ্ক $f_{\text{0}}$ হয়।

পর্যবেক্ষিত কম্পাঙ্ক	কম্পাঙ্কের পরিবর্তন
টেমপ্লেট:Center	টেমপ্লেট:Center

যেখানে,

• $\mathrm{\Delta }f=f-f_0$
• $\mathrm{\Delta }v=-(v_{\text{r}}-v_{\text{s}})$ উৎসের সাপেক্ষে গ্রাহকের আপেক্ষিক গতির বিপরীত; উৎস এবং গ্রাহক একে অপরের দিকে অগ্রসর হলে এটি ধনাত্মক হয়। 

প্রমাণঃ

দেয়া আছে $f=\left(\frac{c+v_{\text{r}}}{c+v_{\text{s}}}\right)f_0$

$c$ দ্বারা ভাগ করে $$f=\left(\frac{1+\frac{v_{\text{r}}}{c}}{1+\frac{v_{\text{s}}}{c}}\right)f_0=(1+\frac{v_{\text{r}}}{c})\left(\frac{1}{1+\frac{v_{\text{s}}}{c}}\right)f_0$$

যেহেতু $\frac{v_{\text{s}}}{c}\ll 1$ আমরা সমীকরণটিকে নিম্নোক্তভাবে লিখতে পারি: $$\frac{1}{1+\frac{v_{\text{s}}}{c}}\approx 1-\frac{v_{\text{s}}}{c}$$

• 
  স্থির শব্দের উৎস একটি ধ্রুবক কম্পাঙ্কে টেমপ্লেট:Math শব্দ তরঙ্গ উৎপন্ন করে এবং তরঙ্গমুখগুলি একটি ধ্রুব গতিতে উৎস থেকে প্রতিসমভাবে দূরে পাঠায়। তরঙ্গমুখের মধ্যবর্তী দূরত্ব হল তরঙ্গদৈর্ঘ্য। সমস্ত পর্যবেক্ষক একই কম্পাঙ্ক শুনতে পাবেন। এটি উৎসের প্রকৃত কম্পাঙ্কের সমান হবে যেখানে টেমপ্লেট:Math।
• 
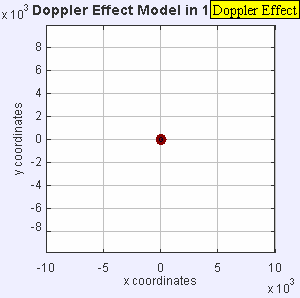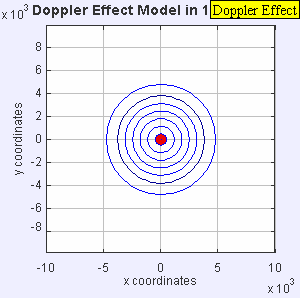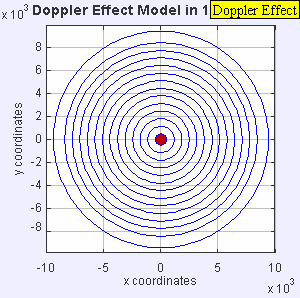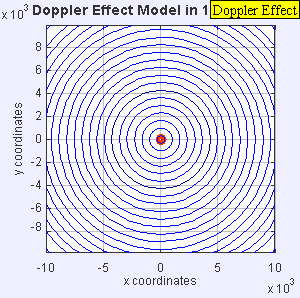
  একই শব্দের উৎস একই মাধ্যমে ধ্রুব কম্পাঙ্কে শব্দ তরঙ্গ বিকিরণ করছে। এসময় শব্দের উৎসের গতি টেমপ্লেট:Math। উৎসটি সরে যাবার কারণে প্রতিটি নতুন তরঙ্গমুখের কেন্দ্র এখন ডানদিকে সামান্য স্থানচ্যুত হয়েছে। ফলস্বরূপ, তরঙ্গমুখগুলি ডান দিকে (সামনে) গুচ্ছবদ্ধ হতে শুরু করে এবং উৎসের বাম দিকে (পিছনে) আরও দূরে ছড়িয়ে পড়ে। একারণে উৎসের সামনে একজন পর্যবেক্ষক উচ্চতর কম্পাঙ্ক শুনতে পাবেন টেমপ্লেট:Math এবং উৎসের পিছনে একজন পর্যবেক্ষক কম কম্পাঙ্ক শুনতে পাবেন টেমপ্লেট:Math।
• 
  এখন উৎসটি মাধ্যমে শব্দের গতিতে চলছে অর্থাৎ (টেমপ্লেট:Math)। উৎসের সামনের তরঙ্গমুখগুলি এখন একই বিন্দুতে গুচ্ছবদ্ধ হয়েছে। ফলে উৎসের সামনে একজন পর্যবেক্ষক উৎসটি না আসা পর্যন্ত কিছুই সনাক্ত করতে পারবে না এবং উৎসের পিছনে থাকা একজন পর্যবেক্ষক কম কম্পাঙ্ক শুনতে পাবেন টেমপ্লেট:Math।
• 
  শব্দের উৎসটি এখন মাধ্যমের শব্দের গতিকে অতিক্রম করে 1.4c গতিতে ভ্রমণ করছে। যেহেতু উৎসটি শব্দ তরঙ্গ তৈরি করে তার চেয়ে দ্রুত গতিতে চলছে, তাই এটি আসলে অগ্রসরমান তরঙ্গের দিকে নিয়ে যায়। পর্যবেক্ষক শব্দ শোনার আগে শব্দ উৎস একটি স্থির পর্যবেক্ষককে অতিক্রম করবে। ফলে উৎসের সামনে একজন পর্যবেক্ষক কিছুই সনাক্ত করবে না এবং উৎসের পিছনে একজন পর্যবেক্ষক কম কম্পাঙ্ক শুনতে পাবে টেমপ্লেট:Math

পরিণতি

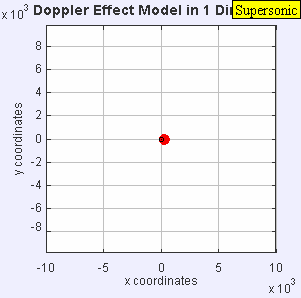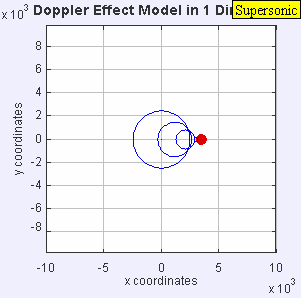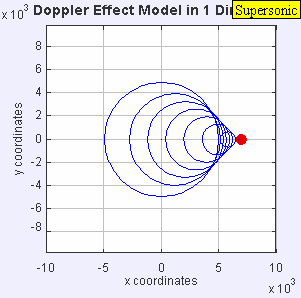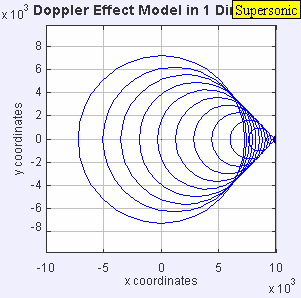
মাধ্যমের সাপেক্ষে একটি পর্যবেক্ষক স্থির থাকলে, যদি একটি চলমান উৎস $f_0$ কম্পাঙ্কের তরঙ্গ নির্গত করে (এক্ষেত্রে, তরঙ্গদৈর্ঘ্য পরিবর্তিত হয়, তরঙ্গ সঞ্চালনের বেগ স্থির থাকে; মনে রাখতে হবে যে তরঙ্গের সঞ্চালনের বেগ উৎসের বেগের উপর নির্ভর করে না), তখন $f$ দ্বারা প্রদত্ত কম্পাঙ্কসহ তরঙ্গ নিম্নোক্ত সমীকরণের সাহায্যে প্রকাশ করা হয়$$f=\left(\frac{c}{c\pm v_{\text{s}}}\right)f_0$$একটি চলমান পর্যবেক্ষক এবং একটি স্থির উৎসের জন্যও অনুরূপ বিশ্লেষণ প্রযোজ্য (এক্ষেত্রে, তরঙ্গদৈর্ঘ্য স্থির থাকে, কিন্তু গতির কারণে তরঙ্গ সঞ্চালনের বেগ [পর্যবেক্ষকের ক্ষেত্রে] পরিবর্তিত হয়)। পর্যবেক্ষণ করা কম্পাঙ্ক থেকে লেখা যায়:$$f=\left(\frac{c\pm v_{\text{r}}}{c}\right)f_0$$একটি স্থির পর্যবেক্ষক এবং শব্দের গতিতে চলমান একটি উৎসের জন্য ডপলার সমীকরণটি শব্দের গতিতে চলমান একটি উৎসের সামনে একজন পর্যবেক্ষকের দ্বারা অনুভূত ক্ষণস্থায়ী অসীম কম্পাঙ্কের পূর্বাভাস দেয়। সব তরঙ্গশীর্ষ একই জায়গায় হওয়ায় তরঙ্গদৈর্ঘ্য শূন্য এবং কম্পাঙ্ক অসীম হয়। তরঙ্গগুলো একটি শক ওয়েভ তৈরি করে, যা 'শব্দনিনাদ (সনিক বুম)' নামে পরিচিত।

উৎস যখন তরঙ্গের গতির চেয়ে দ্রুত চলে তখন উৎসটি তরঙ্গকে ছাড়িয়ে যায়। সমীকরণটি নেতিবাচক কম্পাঙ্কে মান দেয়; যেগুলির এই প্রসঙ্গে কোনো বাস্তবিক সম্পর্ক নেই (উৎসটি অতিক্রম না করা পর্যন্ত পর্যবেক্ষক কোনো শব্দ শুনতে পাবে না)।

লর্ড রেলি শব্দের উপর লেখা তার বইতে নিম্নলিখিত প্রভাব সম্পর্কে বলেছিলেন: যদি পর্যবেক্ষক (স্থির) উৎস থেকে শব্দের দ্বিগুণ গতিতে সরে যায়, তবে সেই উৎস থেকে পূর্বে নির্গত একটি শব্দ সঠিক গতি এবং পিচে শোনা যাবে, কিন্তু মনে হবে যে তা উল্টোভাবে বাজানো হচ্ছে।

ব্যবহার

অ্যাকোস্টিক ডপলার কারেন্ট প্রোফাইলার

অ্যাকোস্টিক ডপলার কারেন্ট প্রোফাইলার (এডিসিপি) হল সোনার- এর মতো একটি হাইড্রোঅ্যাকোস্টিক কারেন্ট মিটার, যা পানির কলামের মধ্যে কণা থেকে বিক্ষিপ্ত শব্দ তরঙ্গের ডপলার প্রভাব ব্যবহার করে গভীরতার পরিসরে পানির বর্তমান বেগ পরিমাপ করতে ব্যবহৃত হয়। এডিসিপি শব্দটি বর্তমান প্রোফাইলারদের জন্য একটি সাধারণ শব্দ, যদিও সংক্ষিপ্ত রূপটি ১৯৮০-এর দশকে একটি যন্ত্র সিরিজ থেকে উদ্ভূত হয়ে। এডিসিপি এর কাজের কম্পাঙ্কের পরিসীমা ৩৮ কিলোহার্জ থেকে কয়েক মেগাহার্জ পর্যন্ত হতে পারে। শব্দ ব্যবহার করে বাতাসের গতির প্রোফাইলিংয়ের জন্য ব্যবহৃত ডিভাইসটি সোডার নামে পরিচিত, যা একই নীতিতে কাজ করে।

রোবোটিক্স

চলমান প্রতিবন্ধকতাসহ একটি পরিশীলিত পরিবেশে রোবটগুলির চলাচলে সহায়তা করার জন্য গতিশীল রিয়েল-টাইম পথ পরিকল্পনা ডপলার প্রভাবের সাহায্য নেয়। এই ধরনের অ্যাপ্লিকেশনগুলি প্রতিযোগিতামূলক রোবোটিক্সের জন্য বিশেষভাবে ব্যবহৃত হয়; যেখানে পরিবেশ ক্রমাগত পরিবর্তন হয়, যেমন - রোবোসকার।

সাইরেন

চিত্র:Juli 2016 - Spoedtransport, Huisarts, Brandweer, Politie en Ambulances met spoed in Rotterdam -451.webm একটি চলমান জরুরী গাড়ির সাইরেন তার স্থির পিচের চেয়ে উপরে শুরু হয়, এটি পাশ দিয়ে যাবার সময় সাথে সাথে নীচে যাবে এবং পর্যবেক্ষকের কাছ থেকে সরে যাওয়ার সাথে সাথে এটির স্থির পিচের চেয়ে নীচে চলতে থাকে। জ্যোতির্বিজ্ঞানী জন ডবসন এই প্রভাব সম্পর্কে বলেছেন:

অন্য ভাষায়, সাইরেন সরাসরি পর্যবেক্ষকের কাছে আসলে পিচটি স্থির থাকবে, যতক্ষণ না গাড়িটি তার কাছে আসে স্থির পিচের চেয়ে উঁচুতে এবং তারপরে অবিলম্বে একটি নতুন নিম্ন পিচে চলে যাবে। যেহেতু যানবাহনটি পর্যবেক্ষকের পাশ দিয়ে যাবার সময় রেডিয়াল গতি স্থির থাকে না, বরং তার দৃষ্টি রেখা এবং সাইরেনের বেগের মধ্যে কোণের একটি ফাংশন হিসাবে পরিবর্তিত হয়:$$v_{\text{radial}}=v_{\text{s}}\cos (\theta )$$যেখানে,

$\theta$ = বস্তুর সামনের বেগ এবং বস্তু থেকে পর্যবেক্ষকের দৃষ্টি রেখার মধ্যবর্তী কোণ।

জ্যোতির্বিদ্যা

দূরবর্তী ছায়াপথের একটি সুপারক্লাস্টারের অপটিক্যাল বর্ণালীতে বর্ণালী রেখার সূর্যের তুলনায় (বাম) লোহিত সরণ (ডান)

আলোর মতো ইলেক্ট্রোম্যাগনেটিক তরঙ্গের জন্য ডপলার প্রভাব জ্যোতির্বিজ্ঞানে ব্যাপকভাবে ব্যবহৃত হয়। তারা এবং ছায়াপথগুলি আমাদের কাছে যে গতিতে আসছে বা আমাদের থেকে পিছিয়ে যাচ্ছে তাকে ব্লুশিফ্ট বা রেডশিফ্ট বলে। একটি ঘনিষ্ঠ যুগ্ম তারা, নক্ষত্র এবং ছায়াপথের ঘূর্ণন গতি পরিমাপ করতে বা এক্সোপ্ল্যানেট সনাক্ত করতে ডপলার প্রভাব ব্যবহার করা যেতে পারে। এই প্রভাব সাধারণত খুব ছোট মাত্রায় ঘটে; ফলে চোখের দৃশ্যমান আলোতে লক্ষণীয় তেমন কোনো পার্থক্য থাকে না। জ্যোতির্বিজ্ঞানে ডপলার প্রভাবের ব্যবহার নক্ষত্রের বর্ণালীতে বিচ্ছিন্ন রেখার সুনির্দিষ্ট কম্পাঙ্ক সম্পর্কে জ্ঞানের উপর নির্ভর করে।

কাছাকাছি নক্ষত্রগুলির মধ্যে সূর্যের সাপেক্ষে বৃহত্তম রেডিয়াল বেগ হল +৩০৮ কিমি/সেকেন্ড ((বিডি-১৫°৪০৪১, এলএইচএস ৫২ নামেও পরিচিত, ৮১.৭ আলোকবর্ষ দূরে) এবং −২৬০ কিমি/সেকেন্ড ((উলি ৯৭২২, উলফ ১১০৬ নামেও পরিচিত এবং এলএইচএস ৬৪, ৭৮.২ আলোকবর্ষ দূরে)। ধনাত্মক রেডিয়াল বেগ মানে নক্ষত্রটি সূর্য থেকে সরে যাচ্ছে আর ঋণাত্মক রেডিয়াল বেগ মানে এটি কাছে আসছে।

রেডশিফ্ট স্থানের প্রসারণ পরিমাপ করতেও ব্যবহৃত হয়, তবে এটি আসল ডপলার ক্রিয়া নয়। বরং এটা স্থানের প্রসারণের কারণে লাল স্থানান্তরকে মহাজাগতিক রেডশিফ্ট বলা হয়, যা সাধারণ আপেক্ষিকতার আনুষ্ঠানিকতার অধীনে রবার্টসন-ওয়াকার মেট্রিক থেকে বিশুদ্ধভাবে নেওয়া যেতে পারে। এছাড়াও মহাজাগতিক স্কেলগুলিতে সনাক্তযোগ্য ডপলার প্রভাব রয়েছে, যাকে ভুলভাবে মহাজাগতিক হিসাবে ব্যাখ্যা করা হলে তা রেডশিফ্ট-স্পেস বিকৃতি পর্যবেক্ষণের দিকে পরিচালিত করে।

রাডার

ইউএস আর্মি সৈনিক একটি রাডার বন্দুক ব্যবহার করে, যা দ্রুত গতিতে লঙ্ঘনকারীদের ধরতে ডপলার রাডারের একটি অ্যাপ্লিকেশন।

ডপলার প্রভাব রাডারে সনাক্ত করা কিছু বস্তুর বেগ পরিমাপ করতে ব্যবহৃত হয়। একটি চলমান লক্ষ্যে একটি রাডার রশ্মি গুলি করা হয় – যেমন একটি মোটর গাড়ি, যেহেতু পুলিশ দ্রুতগামী মোটর চালকদের সনাক্ত করতে রাডার ব্যবহার করে। প্রতিটি ক্রমাগত রাডার তরঙ্গকে প্রতিফলিত হওয়ার আগে এবং উৎসের কাছে পুনরায় সনাক্ত করার আগে গাড়িতে পৌঁছানোর জন্য আরও দূরে যেতে হয়। যেহেতু প্রতিটি তরঙ্গকে আরও দূরে যেতে হয়, প্রতিটি তরঙ্গের মধ্যে ব্যবধান বৃদ্ধি পায় এবং ফলশ্রুতিতে তরঙ্গদৈর্ঘ্যও বৃদ্ধি পায়। কিছু ক্ষেত্রে রাডার বিমটি চলন্ত গাড়ির কাছে আসার সাথে সাথে গুলি করা হয়। এক্ষেত্রে পাশাপাশি অবস্থিত প্রতিটি তরঙ্গ কম দূরত্ব ভ্রমণ করে ও তরঙ্গদৈর্ঘ্য হ্রাস করে। উভয় ক্ষেত্রেই ডপলার প্রভাব দ্বারা সঠিকভাবে গাড়ির গতি নির্ধারণ করা হয়। তদুপরি দ্বিতীয় বিশ্বযুদ্ধের সময় বিকশিত প্রক্সিমিটি ফিউজ সঠিক সময়, উচ্চতা, দূরত্ব ইত্যাদিতে বিস্ফোরক বিস্ফোরণের জন্য ডপলার রাডারের উপর নির্ভর করে।টেমপ্লেট:তথ্যসূত্র প্রয়োজন

যেহেতু ডপলার ক্রিয়া লক্ষ্যের উপর তরঙ্গের ঘটনাকে প্রভাবিত করে এবং সেইসাথে রাডারে প্রতিফলিত তরঙ্গকে প্রভাবিত করে, আপেক্ষিক গতিতে চলার কারণে একটি রাডার দ্বারা পরিলক্ষিত কম্পাঙ্কের পরিবর্তন, $\mathrm{\Delta }v$ একই লক্ষ্য থেকে দ্বিগুণ কম্পাঙ্কের একটি তরঙ্গ নির্গত হয়। যাকে নিম্নোক্তভাবে লেখা যায়:$$\mathrm{\Delta }f=\frac{2\mathrm{\Delta }v}{c}{f}_0.$$

চিকিৎসাবিদ্যায়

ক্যারোটিড ধমনীর কালার ফ্লো আল্ট্রাসনোগ্রাফি (ডপলার) – স্ক্যানার ও স্ক্রিন

একটি ইকোকার্ডিওগ্রাম নির্দিষ্ট সীমার মধ্যে ডপলার প্রভাব ব্যবহার করে রক্ত প্রবাহের দিক এবং রক্ত ও কার্ডিয়াক টিস্যুর গতি সঠিকভাবে মূল্যায়ন করতে পারে। তবে এর সীমাবদ্ধতাগুলোর মধ্যে একটি হল আল্ট্রাসাউন্ড রশ্মি যতটা সম্ভব রক্ত প্রবাহের সমান্তরাল হতে হয়। বেগ পরিমাপ করে কার্ডিয়াক ভালভ এলাকা এবং কার্যকারিতা মূল্যায়ন, হৃদপিন্ডের বাম ও ডান দিকের মধ্যে অস্বাভাবিক যোগাযোগ, ভালভ (ভালভুলার রিগারজিটেশন) এর মাধ্যমে রক্ত স্রোত এবং কার্ডিয়াক আউটপুট গণনা করা যায়। গ্যাস-পূর্ণ মাইক্রোবাবল কনট্রাস্ট মিডিয়া ব্যবহার করে কনট্রাস্ট-বর্ধিত আল্ট্রাসাউন্ড বেগ বা অন্যান্য প্রবাহ-সম্পর্কিত চিকিৎসা পরিমাপ উন্নত করতে ব্যবহার করা যেতে পারে।

যদিও "ডপলার" মেডিকেল ইমেজিংয়ে "বেগ পরিমাপ" এর সমার্থক হয়ে উঠেছে, অনেক ক্ষেত্রে এটি পরিমাপ করা প্রাপ্ত সংকেতের কম্পাঙ্ক শিফট (ডপলার শিফট) নয় বরং ফেজ শিফট (যখন প্রাপ্ত সংকেত আসে)।

রক্ত প্রবাহের বেগ পরিমাপ আল্ট্রাসনোগ্রাফির অন্যান্য ক্ষেত্রেও ব্যবহৃত হয় যেমন- প্রসূতি আল্ট্রাসনোগ্রাফি এবং স্নায়ুচিকিৎসাবিজ্ঞান। ডপলার প্রভাবের উপর ভিত্তি করে ধমনী ও শিরাগুলিতে রক্ত প্রবাহের বেগ পরিমাপ স্টেনোসিসের মতো ভাস্কুলার সমস্যা নির্ণয়ের একটি কার্যকর হাতিয়ার।

প্রবাহ পরিমাপ

তরল প্রবাহে বেগ পরিমাপ করার জন্য লেজার ডপলার ভেলোসিমিটার (এলডিভি) এবং অ্যাকোস্টিক ডপলার ভেলোসিমিটার (এডিভি) এর মতো যন্ত্র তৈরি করা হয়েছে। এলডিভিএকটি হালকা রশ্মি নির্গত করে এবং এডিভি একটি অতিস্বনক অ্যাকোস্টিক বিস্ফোরণ নির্গত করে এবং প্রবাহের সাথে চলমান কণা থেকে প্রতিফলনের তরঙ্গদৈর্ঘ্যে ডপলার প্রভাব পরিমাপ করে। প্রকৃত প্রবাহটি পানির বেগ ও ফেজের একটি ফাংশন হিসাবে গণনা করা হয়। এই কৌশল উচ্চ নির্ভুলতা ও উচ্চ ফ্রিকোয়েন্সিতে অ-অনুপ্রবেশকারী প্রবাহ পরিমাপের অনুমতি দেয়।

বেগ পরিমাপ

মূলত মেডিকেল অ্যাপ্লিকেশানগুলিতে বেগ পরিমাপের জন্য (রক্ত প্রবাহ), আল্ট্রাসনিক ডপলার ভেলোসিমেট্রি (ইউডিভি) তৈরি করা হয়েছে। যা ধুলো, গ্যাস বুদবুদ, ইমালশনের মতো সাসপেনশনের কণা ধারণকারী প্রায় যেকোনো তরলগুলিতে বাস্তব সময়ে সম্পূর্ণ বেগ প্রোফাইল পরিমাপ করতে পারে। এক্ষেত্রে প্রবাহ স্পন্দনশীল, দোদুল্যমান, ল্যামিনার বা অশান্ত, স্থির বা ক্ষণস্থায়ী হতে পারে।

স্যাটেলাইট

সম্ভাব্য ডপলার উচ্চতা কোণের নির্ভরতায় স্থানান্তরিত হয় (এলইও: কক্ষপথের উচ্চতা $h$ = ৭৫০ কিমি)। স্থির গ্রাউন্ড স্টেশন।

ডপলার প্রভাবে জ্যামিতি। চলরাশি: ${\overrightarrow{v}}_{\text{mob}}$ সচল স্টেশনের বেগ, ${\overrightarrow{v}}_{\text{Sat}}$ স্যাটেলাইটের বেগ, ${\overrightarrow{v}}_{\text{rel,sat}}$ স্যাটেলাইটের আপেক্ষিক বেগ, $\varphi$ স্যাটেলাইটের উচ্চতা কোণ এবং $\theta$ স্যাটেলাইটের সাপেক্ষে ড্রাইভিং দিক।

সচল চ্যানেলে ডপলার প্রভাব। চলরাশি: $f_c=\frac{c}{{\lambda }_{\mathrm{c}}}$ বাহকের কম্পাঙ্ক, $f_{\mathrm{D},\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{v_{\mathrm{m}\mathrm{o}\mathrm{b}}}{{\lambda }_{\mathrm{c}}}$ সচল স্টেশনের গতিশীলতার কারণে সর্বাধিক ডপলার স্থানান্তর এবং $f_{\mathrm{D},\mathrm{S}\mathrm{a}\mathrm{t}}$ স্যাটেলাইট সরানোর কারণে অতিরিক্ত ডপলার স্থানান্তর।

স্যাটেলাইট ন্যাভিগেশন

ট্রানজিট ও ডরিসের মতো স্যাটেলাইট নেভিগেশনের জন্য ডপলার শিফটকে কাজে লাগানো যেতে পারে।

স্যাটেলাইট যোগাযোগ

স্যাটেলাইট যোগাযোগেও ডপলার ক্রিয়া ব্যবহার করা হয়। দ্রুত চলমান স্যাটেলাইটগুলির একটি গ্রাউন্ড স্টেশনের সাপেক্ষে কয়েক ডজন কিলোহার্টজের ডপলার প্রভাব থাকতে পারে। ডপলার প্রভাবের মাত্রা পৃথিবীর বক্রতার কারণে পরিবর্তিত হয়। গতিশীল ডপলার ট্রান্সমিশনের সময় একটি সংকেতের কম্পাঙ্ক ক্রমান্বয়ে পরিবর্তিত হয়। তাই স্যাটেলাইট একটি ধ্রুবক কম্পাঙ্কের সংকেত পায়। ২০০৫ সালের ক্যাসিনি-হাইগেন্স মিশনের হাইগেন্স প্রোব চালু করার আগে ডপলার প্রভাবের বিষয়টি বিবেচনায় নেয়া হয়নি। তা উপলব্ধি করার পরে টাইটানের কাছে যাওয়ার জন্য প্রোবের গতিপথটি এমনভাবে পরিবর্তিত হয়েছিল যে তা ব্যাপকভাবে ডপলার শিফট হ্রাস করে ক্যাসিনির সাথে সম্পর্কিত গতির দিকে লম্বভাবে ভ্রমণ করেছিল।

প্রত্যক্ষ কক্ষপথের ডপলার স্থানান্তর নিম্নলিখিত সূত্র দ্বারা অনুমান করা যেতে পারে:$$f_{\mathrm{D},\mathrm{d}\mathrm{i}\mathrm{r}}=\frac{v_{\mathrm{m}\mathrm{o}\mathrm{b}}}{{\lambda }_{\mathrm{c}}}\cos \varphi \cos \theta$$যেখানে,

$v_{\text{mob}}$ সচল স্টেশনের গতি,

${\lambda }_{\mathrm{c}}$ বাহকের তরঙ্গদৈর্ঘ্য,

$\varphi$ স্যাটেলাইটের উচ্চতা কোণ এবং

$\theta$ স্যাটেলাইটের সাপেক্ষে ড্রাইভিং দিক।

স্যাটেলাইট সরানোর কারণে অতিরিক্ত ডপলার শিফটকে নিম্নোক্তভাবে বর্ণনা করা যেতে পারে:$$f_{\mathrm{D},\mathrm{s}\mathrm{a}\mathrm{t}}=\frac{v_{\mathrm{r}\mathrm{e}\mathrm{l},\mathrm{s}\mathrm{a}\mathrm{t}}}{{\lambda }_{\mathrm{c}}}$$যেখানে,

$v_{\mathrm{r}\mathrm{e}\mathrm{l},\mathrm{s}\mathrm{a}\mathrm{t}}$ স্যাটেলাইটের আপেক্ষিক গতি।

অডিও

লেসলি স্পিকার সাধারণত বিখ্যাত হ্যামন্ড অর্গানের সাথে যুক্ত একটি বৈদ্যুতিক মোটর ব্যবহার করে একটি লাউডস্পিকারের চারপাশে একটি অ্যাকোস্টিক হর্ন ঘোরানোর মাধ্যমে ডপলার প্রভাব ব্যবহার করে একটি বৃত্তে এর শব্দ পাঠায়। এটি একটি কীবোর্ড নোটের দ্রুত ওঠানামাকারী কম্পাঙ্কে শ্রোতার কানে পৌছায়।

কম্পন পরিমাপ

লেজার ডপলার ভাইব্রোমিটার (এলডিভি) কম্পন পরিমাপের জন্য একটি অ-যোগাযোগ যন্ত্র। এলডিভি থেকে লেজার রশ্মি বস্তুপৃষ্ঠে নির্দেশিত হয় এবং কম্পনের প্রশস্ততা এবং কম্পাঙ্ক পৃষ্ঠের গতির কারণে লেজার রশ্মির কম্পাঙ্কের ডপলার শিফট এর মাধ্যমে বের করা হয়।

ক্রমবর্ধমান জীববিদ্যা

মেরুদণ্ডী ভ্রূণের বিভাজনের সময় জিনের অভিব্যক্তির তরঙ্গ প্রিসোমিটিক মেসোডার্ম জুড়ে প্রবাহিত হয়, যে টিস্যু থেকে কশেরুকা (সোমাইটস) তৈরি হয়। প্রিসোমিটিক মেসোডার্মের পূর্ববর্তী প্রান্তে একটি তরঙ্গ আসার পরে একটি নতুন সোমাইট তৈরি হয়। জেব্রাফিশে দেখা গিয়েছে যে বিভাজনের সময় প্রিসোমিটিক মেসোডার্মের সংক্ষিপ্তকরণ ডপলারের মতো প্রভাবের দিকে নিয়ে যায় কারণ টিস্যুর অগ্রভাগ তরঙ্গের মধ্যে চলে যায়। এই প্রভাব বিভাজনের সময় অবদান রাখে।

ইনভার্স ডপলার প্রভাব

১৯৬৮ সাল থেকে ভিক্টর ভেসেলাগোর মতো বিজ্ঞানীরা একটি ইনভার্স ডপলার প্রভাবের সম্ভাবনা সম্পর্কে অনুমান করেছেন। ডপলার প্রভাব একটি তরঙ্গ যে মাধ্যমটির মধ্য দিয়ে যাচ্ছে তার প্রতিসরণ সূচকের উপর নির্ভর করে। কিন্তু কিছু উপাদান নেতিবাচক প্রতিসরণে সক্ষম, যা প্রচলিত ডপলার প্রভাবের বিপরীত দিকে কাজ করে। এই প্রভাব সনাক্তকারী প্রথম পরীক্ষাটি ২০০৩ সালে যুক্তরাজ্যের ব্রিস্টলে নাইজেল সেডন ও ট্রেভর বিয়ারপার্ক পরিচালনা করেছিলেন। পরবর্তীতে ইনভার্স ডপলার প্রভাব কিছু অসঙ্গতিপূর্ণ পদার্থে পরিলক্ষিত হয় এবং একটি ভ্যাভিলভ-চেরেনকভ শঙ্কুর ভিতরে এ নিয়ে ভবিষ্যদ্বাণী করা হয়।

আরও দেখুন

• লোহিত সরণ

আরো পড়ুন

• ডপলার, সি. (1842)। Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (বাইনারী নক্ষত্রের রঙিন আলো এবং স্বর্গের অন্যান্য কিছু তারা সম্পর্কে)। প্রকাশক: Abhandlungen der Königl. বোহম Gesellschaft der Wissenschaften (V. Folge, Bd. 2, S. 465–482) [প্রসিডিংস অফ দ্য রয়্যাল বোহেমিয়ান সোসাইটি অফ সায়েন্সেস (Part V, Vol 2)]; প্রাগ: 1842 (পুনরায় প্রকাশিত 1903)। কিছু সূত্র 1843-কে প্রকাশের বছর হিসাবে উল্লেখ করেছে কারণ সেই বছরে নিবন্ধটি প্রসিডিংস অফ দ্য বোহেমিয়ান সোসাইটি অফ সায়েন্সে প্রকাশিত হয়েছিল। ডপলার নিজেই প্রকাশনাটিকে "Prag 1842 bei Borrosch und André" হিসাবে উল্লেখ করেছেন, কারণ 1842 সালে তার একটি প্রাথমিক সংস্করণ ছাপা হয়েছিল যা তিনি স্বাধীনভাবে বিতরণ করেছিলেন।
• "ডপলার এবং ডপলার প্রভাব", EN da C. Andrade, Endeavour Vol. XVIII নং 69, জানুয়ারী 1959 (আইসিআই লন্ডন দ্বারা প্রকাশিত)। ডপলারের মূল কাগজ এবং পরবর্তী উন্নয়নের ঐতিহাসিক বিবরণ।
• ডেভিড নল্টে (2020)। ডপলার প্রভাবের পতন এবং উত্থান। পদার্থবিদ্যা আজ, v. 73, pgs. 31 - 35। DOI: 10.1063/PT.3.4429

বহিঃসংযোগ

• টেমপ্লেট:Commons category-inline
• Doppler Effect, ScienceWorld